题目内容
15.已知一个直角三角形的两条直角边分别为3$\sqrt{2}$和2$\sqrt{6}$,求它的面积.分析 根据直角三角形的面积公式是两直角边乘积的一半可以解答本题.
解答 解:∵一个直角三角形的两条直角边分别为3$\sqrt{2}$和2$\sqrt{6}$,
∴它的面积是:$\frac{3\sqrt{2}×2\sqrt{6}}{2}$=3$\sqrt{12}=6\sqrt{3}$,
即它的面积是$6\sqrt{3}$.
点评 本题考查二次根式的应用、三角形的面积,明确直角三角形的面积公式和二次根式的乘法是解答此类问题的关键.

练习册系列答案
相关题目
7.下列说法,正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 邻补角是互补的两个角,互补的两个角也是邻补角 | |
| C. | 如果两个角有公共顶点和一条公共边,那么它们互为邻补角 | |
| D. | 两条直线相交,如果它们所成的邻补角相等,那么一对对顶角也互补 |
4.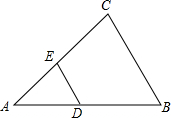 如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
 如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )
如图,在△ABC中,已知DE∥BC,$\frac{AE}{EC}$=$\frac{2}{3}$,则△ADE与△ABC的周长之比为( )| A. | 2:3 | B. | 3:2 | C. | 2:5 | D. | 4:25 |
 如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$.
如图,在Rt△ABC中,∠ACB=90°,CH⊥AB于点H,若BC=5,AC=12,则AB=13,CH=$\frac{60}{13}$.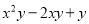 ==______________.
==______________.