题目内容
抛物线y=3x2,y=-3x2,y= x2+3共有的性质是( )
x2+3共有的性质是( )
A.开口向上 B.对称轴是y轴 C.都有最高点 D.y随x值的增大而增大
B
【解析】
试题分析:y=3 开口向上,对称轴为y轴,有最低点,当x<0,y随x的增大而减小,当x>0,y随x的增大而增大;y=-3
开口向上,对称轴为y轴,有最低点,当x<0,y随x的增大而减小,当x>0,y随x的增大而增大;y=-3 开口向下,对称轴为y轴,有最高点,当x<0,y随x的增大而增大,当x>0,y随x的增大而减小;y=
开口向下,对称轴为y轴,有最高点,当x<0,y随x的增大而增大,当x>0,y随x的增大而减小;y=
 +3开口向上,对称轴为y轴,有最低点,当x<0,y随x的增大而减小,当x>0,y随x的增大而增大.所以共有的性质为对称轴是y轴.
+3开口向上,对称轴为y轴,有最低点,当x<0,y随x的增大而减小,当x>0,y随x的增大而增大.所以共有的性质为对称轴是y轴.
考点:二次函数的性质.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
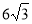 .
.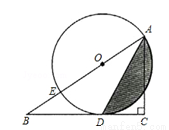
 ,则tanB=_________.
,则tanB=_________.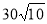 米 D.
米 D.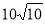 米
米