��Ŀ����
ij������Ʒ�̵�����һ��ɱ�Ϊ50Ԫ�����涨�����ڼ䵥�۲����ڳɱ��ۣ��һ������ø���40%�����������֣�������y�����������۵���x��Ԫ��֮��������ͼ��ʾ��һ�κ�����ϵ��
��1����ȷ��y��x֮��ĺ�����ϵʽ��
��2������������Ʒ�̵������������������õ�����QԪ����д������Q��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ�����������۶�Ϊ����Ԫʱ�����̵�ɻ����������������Ƕ���Ԫ��
��3�������̵����������������õ�������600Ԫ����ȷ�����۵���x��ȡֵ��Χ��
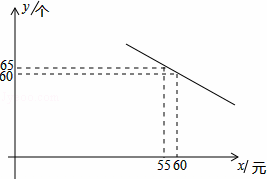


�⣺��1����y=kx+b����������ý�ã�
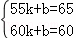
k=��1��b=120��
����һ�κ����ı���ʽΪy=��x+120��
��2������W�����۵���x֮��ĺ�����ϵʽΪ��Q=��x��50������x+120��=��x2+170x��6000��
Q=��x2+170x��6000=����x��85��2+1225��
���Ե��������۶�Ϊ85Ԫʱ�����̵�ɻ�����������������1225Ԫ��
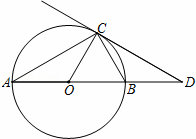
��3����600=��x2+170x��6000��
��ã�x1=60��x2=90��
�������ø���40%��
����۸�Ϊ50��1+50%��=75��
��60��x��75��������
�ʴ�Ϊ��60��x��75��������



��ϰ��ϵ�д�
�����Ŀ

 000Ԫ��
000Ԫ��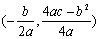 ��3�������۵���Ϊ��
��3�������۵���Ϊ��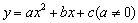 �Ķ��������� ]
�Ķ��������� ]

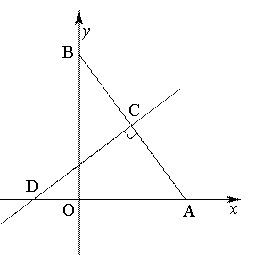
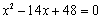 ��������.�߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C����x���ڵ�D.��P��ֱ��CD�ϵ�һ�����㣬��Q��ֱ��AB�ϵ�һ������.
��������.�߶�AB�Ĵ�ֱƽ����CD��AB�ڵ�C����x���ڵ�D.��P��ֱ��CD�ϵ�һ�����㣬��Q��ֱ��AB�ϵ�һ������.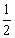 AB��.�����ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�
AB��.�����ڣ���ֱ��д����M�����ꣻ�������ڣ���˵�����ɣ�