题目内容
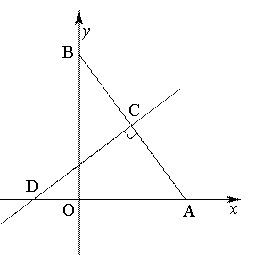
如图,在平面直角坐标系中,已知Rt△AOB的两直角边OA、OB分别在x轴、y轴的正半轴上(OA<OB),且OA、OB的长分别是一元二次方程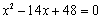 的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D.点P是直线CD上的一个动点,点Q是直线AB上的一个动点.
的两个根.线段AB的垂直平分线CD交AB于点C,交x轴于点D.点P是直线CD上的一个动点,点Q是直线AB上的一个动点.
(1)求A、B两点的坐标;
(2)求直线CD的解析式;
(3)在坐标平面内是否存在点M,使以点C、P、Q、M为顶点的四边形是正方形,且该正方形的边长为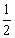 AB长.若存在,请直接写出点M的坐标;若不存在,请说明理由.
AB长.若存在,请直接写出点M的坐标;若不存在,请说明理由.
 |
(1)∵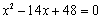
∴x1=6, x2=8
∵OA<OB
∴OA=6,OB=8
∴A(6,0),B(8,0)
(2)根据勾股定理得AB=10
∵CD是AB的垂直平分线
∴AC=5,易求C(3,4)
由于△AOB∽△ACD
∴ ,求得AD=
,求得AD=
∴OD=AD-OA= ∴D(
∴D( ,0)
,0)
由C、D坐标得yCD= x+
x+
(3)存在,M1 (2,-3)M2 (10,3)M3 (4,11)M4(-4,5)

练习册系列答案
相关题目
不等式组﹣2≤x+1<1的解集,在数轴上表示正确的是( )
|
| A. |
| B. |
| C. |
| D. |
|
请你计算:(1﹣x)(1+x),(1﹣x)(1+x+x2),…,猜想(1﹣x)(1+x+x2+…+xn)的结果是( )
|
| A. | 1﹣xn+1 | B. | 1+xn+1 | C. | 1﹣xn | D. | 1+xn |
 = .
= .