题目内容
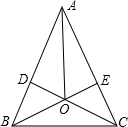 在等腰△ABC中,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD相交于点O,连接OA、BC,试判断直线OA、BC的关系,并说明理由.
在等腰△ABC中,AB=AC,BE⊥AC于E,CD⊥AB于D,BE、CD相交于点O,连接OA、BC,试判断直线OA、BC的关系,并说明理由.考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:证△BDC≌△CEB,推出BE=CD,∠EBC=∠DCB,关键等腰三角形的判定得出OB=OC,求出OD=OE,根据角平分线性质得出AO平分∠BAC,根据等腰三角形的性质得出即可.
解答:解:AO⊥BC,
理由是:∵BE⊥AC,CD⊥AB,
∴∠CDB=∠BEC=90°,
∵AB=AC,
∴∠DBC=∠ECB,
在△BDC和△CEB中,
,
∴△BDC≌△CEB(AAS),
∴BE=CD,∠EBC=∠DCB,
∴OB=OC,
∴OD=OE,
∵BE⊥AC,CD⊥AB,
∴AO平分∠BAC,
∵AB=AC,
∴AO⊥BC.
理由是:∵BE⊥AC,CD⊥AB,
∴∠CDB=∠BEC=90°,
∵AB=AC,
∴∠DBC=∠ECB,
在△BDC和△CEB中,
|
∴△BDC≌△CEB(AAS),
∴BE=CD,∠EBC=∠DCB,
∴OB=OC,
∴OD=OE,
∵BE⊥AC,CD⊥AB,
∴AO平分∠BAC,
∵AB=AC,
∴AO⊥BC.
点评:本题考查了全等三角形的性质和判定,等腰三角形的性质和判定,角平分线性质的应用,解此题的关键是求出AO平分∠BAC,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL等,全等三角形的对应边相等,对应角相等.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )
如图,点P1、P2、P3分别是双曲线同一支图象上的三点,过这三点分别作y轴的垂线,垂足分别是A1、A1、A3,得到的三个三角形△P1A1O、△P2A2O、△P3A3O.设它们的面积分别为S1、S2、S3,则它们的大小关系是( )| A、S1>S2>S3 |
| B、S3>S2>S1 |
| C、S1=S2=S3 |
| D、S2>S3>S1 |
 如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证:
如图,P是正△ABC的边CB延长线上一点,Q是BC延长线上一点,∠PAQ=120°.求证: 如图,抛物线y=-
如图,抛物线y=- 在四边形ABCD中,AB=AC,∠BAC=∠BDC=90°,若BD=3,DC=1,则AD=
在四边形ABCD中,AB=AC,∠BAC=∠BDC=90°,若BD=3,DC=1,则AD=