题目内容
 如图,⊙O的半径为6,弦AB=8,C是圆上一点,求tan∠ACB的值.
如图,⊙O的半径为6,弦AB=8,C是圆上一点,求tan∠ACB的值.考点:圆周角定理,锐角三角函数的定义
专题:
分析:由BC是直径,根据直径所对的圆周角是直角,即可得∠A=90°,然后由勾股定理求得AC的长,继而求得tan∠ACB的值.
解答:解:∵BC是直径,
∴∠A=90°,
∵⊙O的半径为6,弦AB=8,
∴BC=12,
∴AC=
=4
,
∴tan∠ACB=
=
=
.
∴∠A=90°,
∵⊙O的半径为6,弦AB=8,
∴BC=12,
∴AC=
| BC2-AB2 |
| 5 |
∴tan∠ACB=
| AB |
| AC |
| 8 | ||
4
|
2
| ||
| 5 |
点评:此题考查了圆周角定理、勾股定理以及三角函数等知识.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
函数y=-
的自变量x的取值范围是( )
| ||
| x-1 |
| A、x<1 | B、x≥1 |
| C、x>1 | D、x≤1 |
 如图,四边形ABCD是圆内接四边形,E是AD延长线上一点,若∠CBA=120°,则∠EDC的大小是( )
如图,四边形ABCD是圆内接四边形,E是AD延长线上一点,若∠CBA=120°,则∠EDC的大小是( )| A、60° | B、120° |
| C、150° | D、130° |
 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上是该图形能折面一个密封的正方体的盒子,共有
如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上是该图形能折面一个密封的正方体的盒子,共有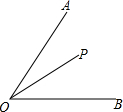 如图,∠AOB=45°,角内一点P,PO=10,两边上各有点Q,R(均不同于O),则△PQR的周长的最小值为
如图,∠AOB=45°,角内一点P,PO=10,两边上各有点Q,R(均不同于O),则△PQR的周长的最小值为 如图,点A、B、C、D在一条直线上,AB=CD,AE∥BF,∠E=∠F.
如图,点A、B、C、D在一条直线上,AB=CD,AE∥BF,∠E=∠F. 如图,CD平分∠BCA,∠1=∠2=30°,你知道∠DEA的度数吗?
如图,CD平分∠BCA,∠1=∠2=30°,你知道∠DEA的度数吗?