题目内容
8．
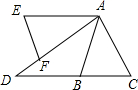如图，将△ABC纸片绕点A按逆时针方向旋转某个角后得到△AEF，CB、AF的延长线交于点D，AE∥CB，∠D=40°，则∠BAC的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
分析 先依据平行线的性质可求得∠EAD的度数，然后依据旋转的性质可求得∠BAC的度数．
解答 解：∵EA∥CB，
∴∠EAD=∠D=40°．
∴由旋转的性质可知：∠BAC=EAD=40°．
故选：B．
点评 本题主要考查的是旋转的性质和平行线的性质，掌握旋转的性质和平行线的性质是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
19．方程组$\left\{\begin{array}{l}{y=x+2}\\{6x+5y=-1}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=0}\\{y=-\frac{1}{5}}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$ |
16．
甲、乙两人在操场上赛跑，他们赛跑的路程S（m）与时间（min）间的函数关系如图所示，则下列说法中正确的个数有（ ）
①甲、乙两人进行1000米赛跑②甲先慢后快，乙先快后慢③比赛到2分钟时，甲、乙两人跑过的路程相等④甲、乙同时到达终点．
甲、乙两人在操场上赛跑，他们赛跑的路程S（m）与时间（min）间的函数关系如图所示，则下列说法中正确的个数有（ ）①甲、乙两人进行1000米赛跑②甲先慢后快，乙先快后慢③比赛到2分钟时，甲、乙两人跑过的路程相等④甲、乙同时到达终点．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
20．下列各数中是有理数的是（ ）
| A． | π | B． | $\sqrt{2}$ | C． | $\sqrt{3}$ | D． | 2 |
如图，在?ABCD中，对角线AC、BD相交于点O，BD=2AD，E、F、G分别是OC、OD、AB的中点，下列结论：①∠OBE=$\frac{1}{2}$∠ADO；②EG=EF；③GF平分∠AGE；④EF⊥GE，其中正确的是①②③．