题目内容
19.已知关于x的一元二次方程x2+2(a-1)x+(a2-a)=0,其中a<0.(1)求证:此方程有两个不相等的实数根.
(2)若等腰三角形ABC的一腰AB长为6,另两边AC,BC的长分别是这个方程的两个不相等的实数根,求等腰三角形ABC的周长.
分析 (1)先计算判别式的值得△,然后根据判别式的意义得到结论;
(2)先利用解方程得方程的解,分别让一个根为6,求得a的数值,得出方程的根,利用三角形的三边关系判定求得△ABC的周长.
解答 解:(1)△=[2(a-1)]2-4(a2-a)=-4a+4,
∵a<0,
∴△>0,
∴方程有两个不相等的实数根;
(2)x2+2(a-1)x+(a2-a)=0,
解得:x1=1-a+$\sqrt{1-a}$,x2=1-a-$\sqrt{1-a}$,
∵等腰△ABC的一腰AB长为6,另两边AC,BC的长分别是这两个方程两个不相等的实数根,
∴当1-a+$\sqrt{1-a}$=6,解得a=-3或-8,
则1-a-$\sqrt{1-a}$=2,
∴等腰△ABC的周长=6+6+2=14;
点评 此题考查一元二次方程的实际运用,掌握解方程的方法,根的判别式,根与系数的关系以及等腰三角形的性质是解决问题的关键.

练习册系列答案
相关题目
9.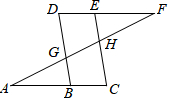 如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
 如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D,则∠A与∠F的大小关系是( )| A. | ∠A+∠F=90° | B. | ∠A>∠F | C. | ∠A<∠F | D. | ∠A=∠F |
10.若a<b<0,则下列各式错误的是( )
| A. | a-2<b-2 | B. | $-\frac{a}{5}<-\frac{b}{5}$ | C. | $\frac{1}{a}>\frac{1}{b}$ | D. | 2a-1<2b-1 |
7.已知a>b,下列不等式中,不一定成立的是( )
| A. | a-5>b-5 | B. | $\frac{1}{2}$a>$\frac{1}{2}$b | C. | 2-3a<2-3b | D. | ma>mb |
4.已知x-2y=3,则代数式6-2x+4y的值为( )
| A. | -3 | B. | -1 | C. | 0 | D. | 3 |
9.2017年的2月共有29天,这个事件是( )
| A. | 随机事件 | B. | 必然事件 | C. | 不可能事件 | D. | 不确定事件 |
