题目内容
若p是三位正数，且（x+a）（x+b）=x2+px+2001，求正整数a、b的值．
考点：多项式乘多项式
专题：
分析：由二次三项式把（x+a）（x+b）化为x2+（a+b）x+ab，再由待定系数法可得a+b=p，ab=2001，再由2001进行分解判断即可．
解答：解：∵（x+a）（x+b）=x2+（a+b）x+ab，
∴a+b=p，ab=2001，
∵a，b是正整数，
∴ab=2001=3×667=1×2001，
又∵p是三位正数，
∴a=3，b=667或a=667，b=3．
∴a+b=p，ab=2001，
∵a，b是正整数，
∴ab=2001=3×667=1×2001，
又∵p是三位正数，
∴a=3，b=667或a=667，b=3．
点评：本题主要考查二次三项式运用，解题的关键是得到a+b=p，ab=2001．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
如图，六边形ABCDEF是⊙O的内接正六边形，P是弧AF上任一点，求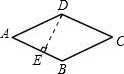
如图，已知菱形ABCD的边长是2，DE⊥AB，垂足为E，∠A=45°，求菱形ABCD的面积．
如图，AD为△ABC的中线，BE⊥AD于E，CF⊥AD于F，求证：DE=DF．