题目内容
1.已知:关于x的函数y=kx2+k2x-2的图象与y轴交于点C,(1)当k=-2时,求图象与x轴的公共点坐标;
(2)若x≥1时函数y随着x的增大而减小,求k的取值范围;
(3)若图象与x轴有一个交点为A,当△AOC是等腰三角形时,求k的值.
分析 (1)当k=-2时,函数为y=-2x2+4x-2,令y=0,求出x的值即可;
(2)首先判断出抛物线开口向下,对称轴在直线x=1的左侧,列出k的不等式,求出k的取值范围;
(3)先求出OC的长,进而求出点A坐标,把点A坐标代入函数y=kx2+k2x-2,即可求出k的值.
解答 解 (1)当k=-2时,函数为y=-2x2+4x-2,
令y=0,则-2x2+4x-2=0,
解得:x1=x2=1,
∴图象与x轴公共点为(1,0).
(2)由“x≥1时函数y随着x的增大而减小”可知,抛物线开口向下,
∴k<0,且对称轴在直线x=1的左侧,
∴-$\frac{{k}^{2}}{2k}$≤1,即$-\frac{k}{2}$≤1,
解不等式组$\left\{\begin{array}{l}{k<0}\\{-\frac{k}{2}≤1}\end{array}\right.$,得-2≤k<0,
(3)当△AOC是等腰三角形时,
∵∠AOC=90°,OC=2,
∴可得OA=OC=2,
∴点A的坐标为(2,0)或(-2,0),
把x=2,y=0代入解析式得2k2+4k-2=0,解得k1=-1+$\sqrt{2}$,k1=-1-$\sqrt{2}$,
把x=-2,y=0代入解析式得-2k2+4k-2=0,解得k1=k1=1,
∴k的值为-1+$\sqrt{2}$或-1-$\sqrt{2}$或1.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是熟练掌握二次函数的性质,解答(2)问时确定对称轴在直线x=1的左侧是关键,此题难度不大.

练习册系列答案
相关题目
11.若火箭发射点火后3秒记为+3秒,那么火箭发射点火前10秒应记为( )
| A. | -10秒 | B. | +10秒 | C. | -3秒 | D. | +3秒 |
9.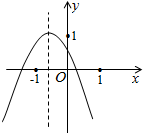 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
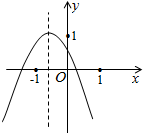 如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )
如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,胡娇同学观察得出了下面四条信息:(1)(a≠0)b2-4ac>0;(2)c>1;(3)2a-b<0;(4)a+b+c<0.你认为其中错误的信息有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
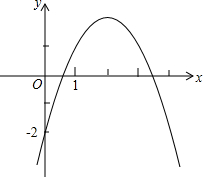 函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.
函数y=ax2+bx+c图象如图,根据图象小明做如下判断:①a<0,b>0,c>0同时成立;②函数值y≤$\frac{4ac-{b}^{2}}{4a}$;③当x$<-\frac{b}{2a}$时,y随x的增大而减小;④a+b+c>0,a-b+c<0,b2-4ac>0同时成立.判断正确的个数为( )个.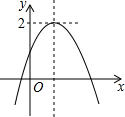 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=2有实数根,有下列结论:①b2-4ac>0;②abc>0;③m≤2.其中,正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=2有实数根,有下列结论:①b2-4ac>0;②abc>0;③m≤2.其中,正确结论的个数是( )
 如图,矩形ABCD中,AD=2AB
如图,矩形ABCD中,AD=2AB