题目内容
方程x2-6x+8=0的两根是三角形的边,则三角形的第三条边长可以是( )
| A、2 | B、4 | C、6 | D、8 |
考点:解一元二次方程-因式分解法,三角形三边关系
专题:
分析:先求出方程的解,求出第三边的取值范围,再判断即可.
解答:解:解方程x2-6x+8=0得:x1=2,x2=4,
即方程的两边是2和4,
设第三边为x,
则4-2<x<2+4,
2<x<6,
∴只有选项B中的数符合,
故选B
即方程的两边是2和4,
设第三边为x,
则4-2<x<2+4,
2<x<6,
∴只有选项B中的数符合,
故选B
点评:本题考查了三角形的三边关系定理,解一元二次方程的应用,解此题的关键是求出第三边的取值范围.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,AB是半圆的直径,点D是弧AC的中点,∠B=50°,则下列判断不正确的是( )
如图,AB是半圆的直径,点D是弧AC的中点,∠B=50°,则下列判断不正确的是( )| A、∠ACB=90° |
| B、AC=2CD |
| C、∠DAB=65° |
| D、∠DAB+∠DCB=180° |
某班抽6名同学参加体能测试,成绩分别是80,90,75,75,80,80.则这组同学的测试成绩的中位数是( )
| A、75 | B、80 | C、85 | D、90 |
在下列方程中,是一元二次方程的是( )
| A、x+y=0 | ||
| B、x+5=0 | ||
| C、x2-2014=0 | ||
D、x-
|
 a,b两个实数在数轴上的对应点如图:下列不等式正确的是( )
a,b两个实数在数轴上的对应点如图:下列不等式正确的是( )| A、a-b>0 |
| B、b-a<0 |
| C、ab-b>0 |
| D、a+ab<0 |
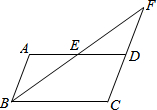 如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是
如图,在?ABCD中,E是AD边上的中点,连接BE,并延长BE交CD延长线于点F,则△EDF与△BCF的周长之比是