题目内容
在△ABC中,AB=5cm,BC=6cm,BC边上的中线AD=4cm,则∠ADC的度数是( )
| A、60° | B、90° |
| C、120° | D、150° |
考点:勾股定理的逆定理
专题:
分析:根据题意画出图形,根据中线的定义,求出BD,由勾股定理的逆定理判断出△ABD为直角三角形,从而求得∠ADC的度数.
解答: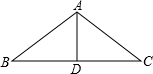 解:∵AB=5cm,BC=6cm,AD=4cm,
解:∵AB=5cm,BC=6cm,AD=4cm,
又∵AD为BC边上的中线,
∴BD=6×
=3,
∴AB2=AD2+BD2,
∴△ABC为直角三角形,
∴∠ADC=∠ADB=90°.
故选B.
 解:∵AB=5cm,BC=6cm,AD=4cm,
解:∵AB=5cm,BC=6cm,AD=4cm,又∵AD为BC边上的中线,
∴BD=6×
| 1 |
| 2 |
∴AB2=AD2+BD2,
∴△ABC为直角三角形,
∴∠ADC=∠ADB=90°.
故选B.
点评:本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
下列计算中,正确的是( )
A、
| ||||||||||||
B、3+4
| ||||||||||||
C、2
| ||||||||||||
D、
|
已知正比例函数y=(k+2)x,且y随x的增大而减小,则k的取值范围是( )
| A、k>2 | B、k>-2 |
| C、k<2 | D、k<-2 |
下列各式中,不是最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
10,20,40,20,80,90,50,40,40,50这10个数据最大值与最小值的差是( )
| A、40 | B、70 | C、80 | D、90 |
 如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x的值为( )
如图,以点O为圆心,OB为半径画弧,交数轴于点A,若点A所表示的数为x,则x的值为( )A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
关于函数y=kx+b(k,b都是不等于0的常数),下列说法,正确的是( )
| A、y与x成正比例 |
| B、y与kx成正比例 |
| C、y与x+b成正比例 |
| D、y-b与x成正比例 |