题目内容
 如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③若OB平分∠AOC,则OC平分∠BOD;④∠AOD的平分线与∠BOC的平分线是同一条射线,其中正确的是
如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:①∠AOB=∠COD;②∠AOB+∠COD=90°;③若OB平分∠AOC,则OC平分∠BOD;④∠AOD的平分线与∠BOC的平分线是同一条射线,其中正确的是考点:角平分线的定义
专题:
分析:根据角的计算和角平分线性质,对四个结论逐一进行计算即可.
解答:解:①∵∠AOC=∠BOD=90°,
∴∠AOB=90°-∠BOC,∠COD=90°-∠BOC,
∴∠AOB=∠COD;
故①正确.
②只有当OB,OC分别为∠AOC和∠BOD的平分线时,∠AOB+∠COD=90°;
故②错误.
③∵∠AOC=∠BOD=90°,OB平分∠AOC,
∴∠AOB=∠COB=45°,则∠COD=90°-45°=45°
∴CB平分∠BOD;
故③正确.
④∵∠AOC=∠BOD=90°,∠AOB=∠COD(已证);
∴∠AOD的平分线与∠COB的平分线是同一条射线.
故④正确.
故答案为:①②③.
∴∠AOB=90°-∠BOC,∠COD=90°-∠BOC,
∴∠AOB=∠COD;
故①正确.
②只有当OB,OC分别为∠AOC和∠BOD的平分线时,∠AOB+∠COD=90°;
故②错误.
③∵∠AOC=∠BOD=90°,OB平分∠AOC,
∴∠AOB=∠COB=45°,则∠COD=90°-45°=45°
∴CB平分∠BOD;
故③正确.
④∵∠AOC=∠BOD=90°,∠AOB=∠COD(已证);
∴∠AOD的平分线与∠COB的平分线是同一条射线.
故④正确.
故答案为:①②③.
点评:此题主要考查学生对角的计算,角平分线的理解和掌握,此题难度不大,属于基础题.

练习册系列答案
相关题目
在Rt△ABC中,∠C=90°,若AB=
,BC=2,则sinB的值为( )
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
下列说法正确的有( )
①对角线相等且互相垂直的四边形是菱形
②邻边相等的平行四边形是正方形
③对角线相等且互相平分的四边形是矩形
④顺次连接菱形各边中点所得的四边形是矩形
⑤有一个内角是60°的平行四边形是菱形.
①对角线相等且互相垂直的四边形是菱形
②邻边相等的平行四边形是正方形
③对角线相等且互相平分的四边形是矩形
④顺次连接菱形各边中点所得的四边形是矩形
⑤有一个内角是60°的平行四边形是菱形.
| A、1个 | B、2个 | C、3个 | D、4个 |
等腰三角形一腰上的高与另一腰的夹角为60°,则顶角的度数为( )
| A、30° |
| B、60° |
| C、60°或120° |
| D、30°或150° |
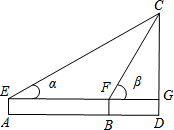 小红想要测量校园内一座教学楼CD的高度.她先在A处测得楼顶C的仰角α=30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角β=60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米)参考数据:
小红想要测量校园内一座教学楼CD的高度.她先在A处测得楼顶C的仰角α=30°,再向楼的方向直行10米到达B处,又测得楼顶C的仰角β=60°,若小红的目高(眼睛到地面的高度)AE为1.60米,请你帮助她计算出这座教学楼CD的高度(结果精确到0.1米)参考数据: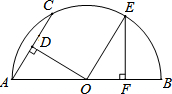 如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( ) 为了维护海洋权益,新组建的国家海洋局加强了海洋巡逻力度,如图,一艘海监船位于灯塔P的南向东45°方向,距离灯塔200海里的A处,沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处.
为了维护海洋权益,新组建的国家海洋局加强了海洋巡逻力度,如图,一艘海监船位于灯塔P的南向东45°方向,距离灯塔200海里的A处,沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处.