题目内容
已知w、x、y、z四个数都不等于0,也互不相等,如果w+
=x+
=y+
=z+
,那么w2x2y2z2= .
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| w |
考点:对称式和轮换对称式
专题:
分析:先根据w+
=x+
=y+
=z+
分别表示出w-x,x-y,y-z,z-w的值,再把这四个式子进行相乘,即可求出w2x2y2z2的值.
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| w |
解答:解:∵w+
=x+
,
∴w-x=
-
=
,
同理可得:
x-y=
-
=
,
y-z=
,
z-w=
,
∴(w-x)(x-y)(y-z)(z-w)=
•
•
•
=
∴w2x2y2z2=1.
故答案为:1.
| 1 |
| x |
| 1 |
| y |
∴w-x=
| 1 |
| y |
| 1 |
| x |
| x-y |
| xy |
同理可得:
x-y=
| 1 |
| z |
| 1 |
| y |
| y-z |
| yz |
y-z=
| z-w |
| zw |
z-w=
| w-x |
| wx |
∴(w-x)(x-y)(y-z)(z-w)=
| x-y |
| xy |
| y-z |
| yz |
| z-w |
| zw |
| w-x |
| wx |
| (x-y)(y-z)(z-w)(w-x) |
| w2x2y2z2 |
∴w2x2y2z2=1.
故答案为:1.
点评:此题考查了对称式和轮换对称式;解题的关键是通过变形得出(w-x)(x-y)(y-z)(z-w)=
.
| (x-y)(y-z)(z-w)(w-x) |
| w2x2y2z2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
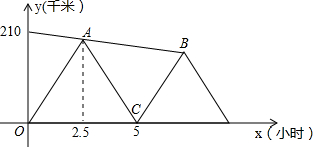 步行速度均近似为匀速,队员上、下车的时间忽略不计).
步行速度均近似为匀速,队员上、下车的时间忽略不计).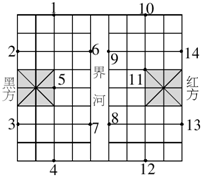 如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?
如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大? 如图,△ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且BD=CE,DE与BC相交于点F.求证:DF=EF.
如图,△ABC中,AB=AC,点D、E分别在AB、AC的延长线上,且BD=CE,DE与BC相交于点F.求证:DF=EF.