题目内容
如图,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为_______.

 .
.
【解析】
试题分析:连接CH,得△CFH≌△CDH(HL),可求∠DCH=30°,在Rt△DCH中利用三角函数可求出DH的长.
试题解析:连接CH.

∵四边形ABCD,四边形EFCG都是正方形,且正方形ABCD绕点C旋转后得到正方形EFCG,
∴∠F=∠D=90°,
∴△CFH与△CDH都是直角三角形,
在Rt△CFH与Rt△CDH中,
∵ ,
,
∴△CFH≌△CDH(HL).
∴∠DCH= ∠DCF=
∠DCF= (90°-30°)=30°.
(90°-30°)=30°.
在Rt△CDH中,CD=3,
∴DH=tan∠DCH×CD= .
.
考点:1.正方形的性质;2.旋转的性质;

练习册系列答案
相关题目
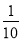 B.
B.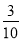 C.
C.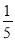 D.
D.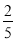

 , 则
, 则 .
.
 m C.4
m C.4 m D.2
m D.2 m
m 