题目内容
12.已知P是⊙O外的一点,且PA、PB是⊙O的两条切线,切点分别为A、B,OP交AB于点C,OP=5,cos∠APC=$\frac{4}{5}$.(1)求⊙O的半径;
(2)求弦AB的长.
分析 (1)由PA为圆O的切线,利用切线的性质得到三角形AOP为直角三角形,根据sin∠APC的值得出sin∠APO的值,利用锐角三角函数定义及OP的长求出OA的长,即为圆的半径;
(2)根据PA、PB是⊙O的两条切线,得到PA=PB,由于OA=OB,推出OP垂直平分AB,根据三角形的面积公式即可求解.
解答 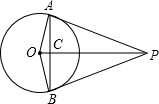 解:(1)∵PA、PB是⊙O的两条切线,
解:(1)∵PA、PB是⊙O的两条切线,
∴∠PAO=90°,
∵cos∠APC=$\frac{4}{5}$,OP=5,
∴AP=4,
∴OA=3;
(2)∵PA、PB是⊙O的两条切线,
∴PA=PB,∵OA=OB,
∴OP垂直平分AB,
∵AC=$\frac{OA•AP}{OP}$=$\frac{12}{5}$,
∴AB=2AC=$\frac{24}{5}$.
点评 此题考查了切线的性质,切线长定理,以及解直角三角形,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
7.边长分别等于6cm、8cm、10cm的三角形的内切圆的半径为( )cm.
| A. | $\sqrt{3}$ | B. | 2 | C. | 3$\sqrt{2}$ | D. | 6 |
4.已知函数y=(k-3)x+k2-9的图象经过坐标原点(0,0),则k的值为( )
| A. | ±3 | B. | 3 | C. | -3 | D. | 以上答案都不对 |
1.下列说法中,正确的是( )
| A. | 两条直线被第三条直线所截,同旁内角互补 | |
| B. | 在同一平面内,两条直线的位置关系是平行、相交与垂直 | |
| C. | 平移前后图形的形状和大小都没有发生改变 | |
| D. | 相等的角是对顶角 |
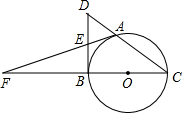 如图 A是以BC为直径的⊙O上一点,过点B作⊙O的切线,与CA的延长线交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.求证:AF是⊙O的切线.
如图 A是以BC为直径的⊙O上一点,过点B作⊙O的切线,与CA的延长线交于点D,E是BD的中点,延长AE与CB的延长线相交于点F.求证:AF是⊙O的切线.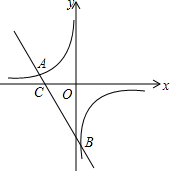 如图所示,直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B,与x轴交于点C.
如图所示,直线y=-2x+b与反比例函数$y=\frac{k}{x}$交于点A、B,与x轴交于点C.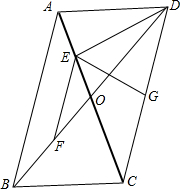 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OA、OB、CD的中点.求证:
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OA、OB、CD的中点.求证: