题目内容
已知直角三角形的两条直角边的长分别为6cm,8cm,则此直角三角形的重心与外心之间的距离是 .
考点:三角形的外接圆与外心,三角形的重心
专题:
分析:利用在Rt△ABC,可求得AB=10cm,根据内切圆的性质可判定四边形OECE是正方形,所以用r分别表示:CE=CD=r,AE=AN=6-r,BD=BN=8-r;再利用AB作为相等关系求出r=2cm,则可得AN=4cm,N为圆与AB的切点,M为AB的中点,根据直角三角形中外接圆的圆心是斜边的中点,即M为外接圆的圆心;在Rt△OMN中,先求得MN=AM-AN=1cm,由勾股定理可求得OM的长.
解答: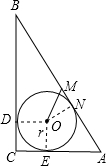 解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,
解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,
∴AB=10cm,
设Rt△ABC的内切圆的半径为r,则OD=OE=r,
∵∠C=90°,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∴8-r+6-r=10,
解得r=2cm,
∴AN=4cm,
在Rt△OMN中,MN=AM-AN=1cm,
∴OM=
cm.
故答案为:
cm.
 解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,
解:如图,在Rt△ABC,∠C=90°,AC=8cm,BC=6cm,∴AB=10cm,
设Rt△ABC的内切圆的半径为r,则OD=OE=r,
∵∠C=90°,
∴CE=CD=r,AE=AN=6-r,BD=BN=8-r,
∴8-r+6-r=10,
解得r=2cm,
∴AN=4cm,
在Rt△OMN中,MN=AM-AN=1cm,
∴OM=
| 5 |
故答案为:
| 5 |
点评:此题考查了直角三角形的外心与内心概念及内切圆的性质,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
某车间有26名工人,每人每天能生产螺栓12个或螺母18个.若要使每天生产的螺栓和螺母按1:2配套,则分配几人生产螺栓?设分配x名工人生产螺栓,其他工人生产螺母,所列方程正确的是( )
| A、12x=18(26-x) |
| B、18x=12(26-x) |
| C、2×18x=12(26-x) |
| D、2×12x=18(26-x) |
 如图,△ABC绕点A旋转到AB′C′,BC与B′C′交于P,试说明AP平分∠BPC′.
如图,△ABC绕点A旋转到AB′C′,BC与B′C′交于P,试说明AP平分∠BPC′. 如图,已知AB∥CD,∠C=55°,∠A=30°,则∠F=
如图,已知AB∥CD,∠C=55°,∠A=30°,则∠F=