Question

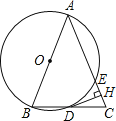
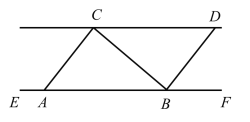
【题目】在数学探究活动中，敏敏进行了如下操作：如图，将四边形纸片沿过点的直线折叠，使得点落在上的点处，折痕为；再将分别沿折叠，此时点落在上的同一点处．请完成下列探究：

的大小为__________；

当四边形是平行四边形时的值为__________．

Answer 1

【答案】30

【解析】

（1）根据折叠得到∠D+∠C=180°，推出AD∥BC，，进而得到∠AQP=90°，以及∠A=180°-∠B=90°，再由折叠，得到∠DAQ=∠BAP=∠PAQ=30°即可；

（2）根据题意得到DC∥AP，从而证明∠APQ=∠PQR，得到QR=PR和QR=AR，结合（1）中结论，设QR=a，则AP=2a，由勾股定理表达出AB=AQ=即可解答．

解：（1）由题意可知，∠D+∠C=180°，

∴AD∥BC，

由折叠可知∠AQD=∠AQR，∠CQP=∠PQR，

∴∠AQR+∠PQR=，即∠AQP=90°，

∴∠B=90°，则∠A=180°-∠B=90°，

由折叠可知，∠DAQ=∠BAP=∠PAQ，

∴∠DAQ=∠BAP=∠PAQ=30°，

故答案为：30；

（2）若四边形APCD为平行四边形，则DC∥AP，

∴∠CQP=∠APQ，

由折叠可知：∠CQP=∠PQR，

∴∠APQ=∠PQR，

∴QR=PR，

同理可得：QR=AR，即R为AP的中点，

由（1）可知，∠AQP=90°，∠PAQ=30°，且AB=AQ，

设QR=a，则AP=2a，

∴QP=，

∴AB=AQ=，

∴，

故答案为：．