Question

【题目】在平面直角坐标系中，已知直线（）与双曲线交于，两点（点在第一象限），直线（）与双曲线交于，两点．当这两条直线互相垂直，且四边形的周长为时，点的坐标为_________．

Answer 1

【答案】或

【解析】

首先根据题意求出点A坐标为(，)，从而得出，然后分两种情况：①当点B在第二象限时求出点B坐标为(，)，从而得出，由此可知，再利用平面直角坐标系任意两点之间的距离公式可知：，所以，据此求出，由此进一步通过证明四边形ABCD是菱形加以分析求解即可得出答案；②当点B在第四象限时，方法与前者一样，具体加以分析即可.

∵直线()与双曲线交于，两点（点在第一象限），

∴联立二者解析式可得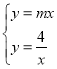：，由此得出点A坐标为(，)，

∴，

①当点B在第二象限时，如图所示：

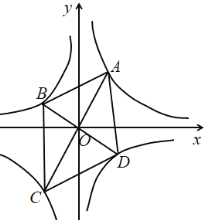
∵直线（）与双曲线交于，两点，

∴联立二者解析式可得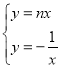：，由此得出点B坐标为(，)，

∴，

∵AC⊥BD，

∴，

根据平面直角坐标系任意两点之间的距离公式可知：

，

∴，

解得：，

∴，

根据反比例函数图象的对称性可知：OC=OA，OB=OD，

∵AC⊥BD，

∴四边形ABCD是菱形，

∴，

∴，

解得：或2，

∴A点坐标为(，)或(，)，

②当点B在第四象限时，如图所示：

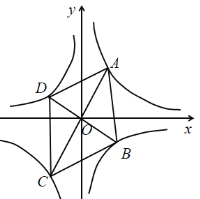
∵直线（）与双曲线交于，两点，

∴联立二者解析式可得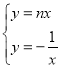：，由此得出点B坐标为(，)，

∴，

∵AC⊥BD，

∴，

根据平面直角坐标系任意两点之间的距离公式可知：

，

∴，

解得：，

∴，

根据反比例函数图象的对称性可知：OC=OA，OB=OD，

∵AC⊥BD，

∴四边形ABCD是菱形，

∴，

∴，

解得：或2，

∴A点坐标为(，)或(，)，

综上所述，点A坐标为：(，)或(，)，

故答案为：(，)或(，).