题目内容
6. 如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,求圆心O到弦BC的距离.
如图,C是以AB为直径的⊙O上一点,已知AB=5,BC=3,求圆心O到弦BC的距离.
分析 作OD⊥BC于D,根据勾股定理求出AC,根据三角形中位线定理计算即可.
解答 解: 作OD⊥BC于D,
作OD⊥BC于D,
∵AB为直径,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
∵OD⊥BC,
∴BD=DC,又OA=OB,
∴OD=$\frac{1}{2}$AC=2.
点评 本题考查的是圆周角定理、垂径定理,掌握半圆(或直径)所对的圆周角是直角、三角形中位线定理是解题的关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
1.股民小胡上星期五以每股13.10元的价格买进某种股票1000股,该股票的涨跌情况如表(单位:元).
(1)星期五收盘时,每股是13.05元;
(2)本周内最高股是每股13.05元,最低股是每股12.75元.
(3)已知小胡买进股票时付了3‰的手续费,卖出时需付成交额3‰的手续费和2‰的交易税.如果小胡在星期五收盘前将全部股票卖出,他的收益如何?
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | -0.29 | +0.06 | -0.12 | +0.24 | +0.06 |
(2)本周内最高股是每股13.05元,最低股是每股12.75元.
(3)已知小胡买进股票时付了3‰的手续费,卖出时需付成交额3‰的手续费和2‰的交易税.如果小胡在星期五收盘前将全部股票卖出,他的收益如何?
18.生活与数学
(1)姆同学在某月的日历上圈出2×2个数,如图1,正方形的方框内的四个数的和是48,那么这四个数是8,9,15,16.
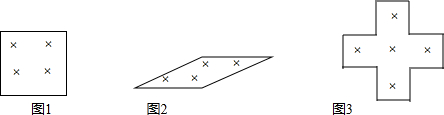
(2)丽也在上面的日历上圈出2×2个数,如图2,斜框内的四个数的和是46,则它们分别是8,9,14,15.
(3)莉也在日历上圈出5个数,呈十字框形,如图3,它们的和是55,则中间的数是11.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是29号?
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |

(2)丽也在上面的日历上圈出2×2个数,如图2,斜框内的四个数的和是46,则它们分别是8,9,14,15.
(3)莉也在日历上圈出5个数,呈十字框形,如图3,它们的和是55,则中间的数是11.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是29号?
 在△ABC与△PQM中,AD⊥BC,PE⊥QM,AD=PE,CD=EM,∠B=∠Q.
在△ABC与△PQM中,AD⊥BC,PE⊥QM,AD=PE,CD=EM,∠B=∠Q.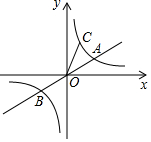 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,则点B的坐标为(-4,-2),△AOC的面积为15.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于A,B两点,且点A的横坐标为4,双曲线y=$\frac{k}{x}$(k>0)上一点C的纵坐标为8,则点B的坐标为(-4,-2),△AOC的面积为15.