题目内容
13．长方形的长是3$\sqrt{2}$，宽是$\sqrt{6}$，则面积是6$\sqrt{3}$，对角线长是2$\sqrt{6}$．分析 根据长方形的面积公式和勾股定理可以解答本题．
解答 解：∵长方形的长是3$\sqrt{2}$，宽是$\sqrt{6}$，
∴长方形的面积是：$3\sqrt{2}×\sqrt{6}$=6$\sqrt{3}$，
对角线的长是：$\sqrt{（3\sqrt{2}）^{2}+（\sqrt{6}）^{2}}$=$\sqrt{18+6}=\sqrt{24}=2\sqrt{6}$，
故答案为：$6\sqrt{3}$，$2\sqrt{6}$．
点评 本题考查二次根式的应用，解题的关键是明确长方形的面积公式和勾股定理．
练习册系列答案
相关题目
如图，一次函数y=kx+b与y=x+5的图象相交于点P（-3，m），则方程组$\left\{\begin{array}{l}{y=kx+b}\\{y=x+5}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$．
元旦晚会上，小刚用一张半径为25cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面（接缝忽略不计），如果做成的圆锥形小丑帽子的底面半径为10cm，那么这张扇形纸板的圆心角应为144度．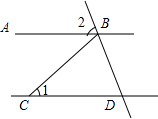
如图所示，AB∥CD，BC=CD，∠1=40°，则∠2的度数为70°．
△ABC，∠B=∠C=30°，P为BC中点，∠MPN=30°，求证：△BPM∽△CNP∽△PNM；MP平分∠BMN；NP平分∠CNM；MN=BM+CN-$\frac{3}{2}$AB；BM•CN=$\frac{3}{4}$AB2．