题目内容
如图，抛物线y=ax2+bx+c（a≠0）与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．
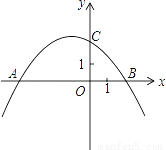
（1）求抛物线的解析式；
（2）若点D为该抛物线上的一个动点，且在直线AC上方，当以A、C、D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；
（3）以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．
（1）y=﹣x2﹣x+2；（2）2，D的坐标为（﹣2，2）；（3）y=x﹣或y=﹣x﹣． 【解析】试题分析： （1）由已知条件可设抛物线解析式为： ，再代入点C的坐标（0，2）解得的值即可得到抛物线的解析式； （2）如图2，过点D作DH⊥AB于H，交直线AC于点G，由A、C的坐标求出直线AC的解析式，设点D的横坐标为“m”，则可用含“m”的代数式表达出DG的长，结合S△ADC=D...
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
九年级某班40位同学的年龄如表所示：
年龄（岁） | 13 | 14 | 15 | 16 |
人数 | 3 | 16 | 19 | 2 |
则该班40名同学年龄的众数和中位数分别是________．
15,15 【解析】观察、分析表格中的数据可知：（1）出现次数最多的是15岁；（2）把年龄从小到大排列可知，排在第20位和21位的年龄都是15岁； ∴该班40名同学年龄的众数是15岁，中位数也是15岁.