Question

10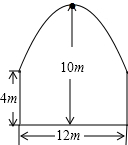．如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m，隧道顶部最高点距地面10m．在抛物线型拱壁上需要安装两排灯．使它们离地面的高度相等，如果灯离地面的高度为8m，那么两排灯之间的水平距离是多少米？

Answer 1

分析 先建立如图所示的平面直角坐标系，求出抛物线的解析式，根据灯离地面的高度为8m，得出点B的纵坐标，代入解析式中列一元二次方程求出x的值，因为A、B是对称点，所以点A的横坐标与点B的横坐标的绝对值相等，由此得出AB=4$\sqrt{3}$米．

解答 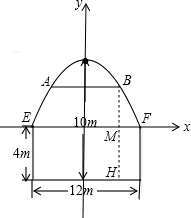解：建立如图所示的平面直角坐标系，则抛物线的顶点C（0，6），
设抛物线的解析式为：y=ax²+6，
由题意得：F（6，0），
把F（6，0）代入y=ax²+6中得：0=36a+6，
a=-$\frac{1}{6}$，
∴抛物线的解析式为：y=-$\frac{1}{6}$x²+6，
过B作BH⊥DG，垂足为H，交x轴于M，则BH⊥x轴，
因为灯离地面的高度为8m，
所以BM=BH-HM=8-4=4，
当y=4时，-$\frac{1}{6}$x²+6=4，
x=$±2\sqrt{3}$，
∴AB=2$\sqrt{3}$×2=4$\sqrt{3}$，
答：两排灯之间的水平距离是4$\sqrt{3}$米．

点评 本题是二次函数的实际应用问题，属于隧道问题；此类问题要建立恰当的平面直角坐标系，建立坐标系时要使隧道所成的抛物线的解析式最简单，运用已知条件求出相应的结论，在解题时注意点的坐标特点和线段的长．