题目内容
9.已知关于x的一元二次方程x2-4x+c=0.(1)当实数c<4时,该方程有两个不等实根;
(2)如2+$\sqrt{3}$是该方程的一个根,则实数c的值是-1
(3)在(2)的条件下,解方程求该方程的另一个根.
分析 (1)根据判别式的作用即可求出答案.
(2)将x=2+$\sqrt{3}$代入x2-4x+c=0即可求出c的值.
(3)由根与系数的关系即可求出答案.
解答 解:(1)△=16-4c>0,
∴c<4
(2)将x=2+$\sqrt{3}$代入x2-4x+c=0,
∴(2+$\sqrt{3}$)2-4(2+$\sqrt{3}$)+c=0,
7+4$\sqrt{3}$-8-4$\sqrt{3}$+c=0
c=-1
(3)设方程的另外一个根为x,
由根与系数的关系可知:x+2+$\sqrt{3}$=4
∴x=2-$\sqrt{3}$
故答案为:(1)c<4;(2)-1
点评 本题考查一元二次方程的相关知识,解题的关键是熟练运判别式以及根与系数的关系,本题属于基础题型.

练习册系列答案
相关题目
19. 如图,关于线段、射线、直线的条数,说法正确的是( )
如图,关于线段、射线、直线的条数,说法正确的是( )
 如图,关于线段、射线、直线的条数,说法正确的是( )
如图,关于线段、射线、直线的条数,说法正确的是( )| A. | 五条线段,三条射线 | B. | 一条射线,三条线段 | ||
| C. | 三条线段,三条射线 | D. | 三条线段,两条射线,一条直线 |
18.-|x|的相反数是( )
| A. | |x| | B. | $\frac{1}{|x|}$ | C. | -|x| | D. | -$\frac{1}{|x|}$ |
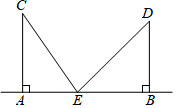 为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等.
为了推广城市绿色出行,南沙区交委准备在蕉门河沿岸东西走向AB路段建设一个共享单车停放点,该路段附近有两个广场C和D,如图所示,CA⊥AB于A,DB⊥AB于B,AB=3km,CA=2km,DB=1.6km,试问这个单车停放点E应建在距点A多少km处,才能使它到两广场的距离相等. 如图直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=60°,则∠2=105°.
如图直线l1∥l2,一块含45°角的直角三角板如图所示放置,∠1=60°,则∠2=105°. 如图,OC平分∠AOB,D为OC上一点,DE⊥OB于E,若DE=5,则D到OA的距离为5.
如图,OC平分∠AOB,D为OC上一点,DE⊥OB于E,若DE=5,则D到OA的距离为5.