题目内容
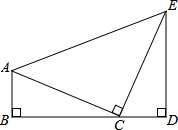 AB、ED分别垂直于BD,点B、D是垂足,点C是BD上一点,△ACE是等腰三角形,且∠ACE=90°,求证:BD=AB+ED.
AB、ED分别垂直于BD,点B、D是垂足,点C是BD上一点,△ACE是等腰三角形,且∠ACE=90°,求证:BD=AB+ED.考点:全等三角形的判定与性质,等腰直角三角形
专题:证明题
分析:利用同角的余角相等得到一对角相等,再由一对直角相等,AC=EC,利用AAS得到三角形ABC与三角形CDE全等,利用全等三角形的对应边相等得到AB=CD,BC=ED,由BD=BC+CD,等量代换即可得证.
解答:证明:∵∠ACE=90°,
∴∠ACB+∠DCE=90°,
∵∠ACB+∠BAC=90°,
∴∠DCE=∠BAC,
∵△ACE为等腰直角三角形,
∴AC=EC,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS),
∴AB=CD,BC=ED,
则BD=BC+CD=ED+AB.
∴∠ACB+∠DCE=90°,
∵∠ACB+∠BAC=90°,
∴∠DCE=∠BAC,
∵△ACE为等腰直角三角形,
∴AC=EC,
在△ABC和△CDE中,
|
∴△ABC≌△CDE(AAS),
∴AB=CD,BC=ED,
则BD=BC+CD=ED+AB.
点评:此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
有一批苹果需要装箱,若每箱装25千克,则有40千克装不下;若每箱装30千克,则剩余20只空箱,这批苹果共有( )
| A、2760千克 |
| B、112千克 |
| C、3240千克 |
| D、128千克 |
为了了解某厂产品的合格率,随机抽查了1000件产品进行质量检测分析,关于这一问题说法中正确的是( )
| A、总体是指该厂生产的所有产品 |
| B、个体是指100件产品中的每一件 |
| C、这种调查方式是抽样调查 |
| D、样本是指这1000件产品 |
 如图:直线a,b,c被直线d所截,且a∥b,c∥b.求证:a∥c(利用公理:两直线平行,同位角相等来证)
如图:直线a,b,c被直线d所截,且a∥b,c∥b.求证:a∥c(利用公理:两直线平行,同位角相等来证)