��Ŀ����
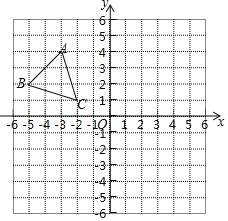
����Ŀ����֪�ȱ���ABC�͵�P�����P����ABC����AB��AC��BC�ľ���ֱ�Ϊh1��h2��h3����ABC�ĸ�Ϊh��
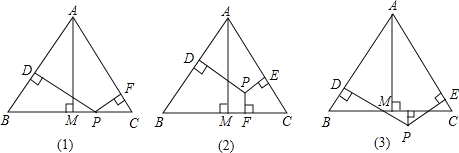
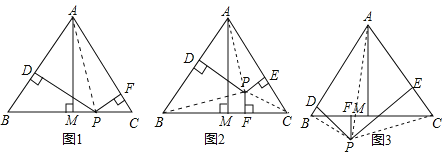
��1������P��һ��BC�ϣ���ͼ�٣���ʱh3��0����֤��h1+h2+h3��h��
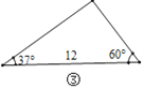
��2������P����ABC�ڣ���ͼ�ڣ��Լ���P����ABC�⣬��ͼ�ۣ����������ʱ�����������Ƿ��������������������֤��������������h1��h2��h3��h֮�����������Ĺ�ϵ����˵����IJ��룬��˵�����ɣ�
���𰸡���1������������2����P����ABC��ʱ��������P�ڡ�ABC��ʱ�����������ɼ�����.
��������
(1)����AP,����ABC����ֳɡ�ABP�͡�APC�����,���������ʽ���뼴��֤��.
(2)����AP��BP��CP,����ABC��������ѳɼ���С�����ε����֮��,���������ʽ���㼴��.
��1����ͼ1������AP���� S��ABC��S��ABP+S��APC
��![]() BCAM��
BCAM��![]() ABPD+
ABPD+![]() ACPF
ACPF
��![]() BCh��
BCh��![]() ABh1+
ABh1+![]() ACh2
ACh2
�֡ߡ�ABC�ǵȱ�������
��BC��AB��AC��
��h��h1+h2��
��2����P�ڡ�ABC��ʱ��h��h1+h2+h3���������£�
��ͼ2������AP��BP��CP���� S��ABC��S��ABP+S��BPC+S��ACP
��![]() BCAM��
BCAM��![]() ABPD+
ABPD+![]() ACPF+
ACPF+![]() BCPE
BCPE
��![]() BCh��
BCh��![]() ABh1+
ABh1+![]() ACh2+
ACh2+![]() BCh3
BCh3
�֡ߡ�ABC�ǵȱ������Σ�
��BC��AB��AC��
��h��h1+h2+h3��
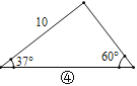
��P�ڡ�ABC��ʱ��h��h1+h2��h3��
�������£���ͼ3������PB��PC��PA
�������ε������ʽ�ã�S��ABC��S��PAB+S��PAC��S��PBC��
��![]() BCAM��
BCAM��![]() ABPD+
ABPD+![]() ACPE��
ACPE��![]() BCPF��
BCPF��
��AB��BC��AC��
��h1+h2��h3��h��
��h1+h2��h3��h��