题目内容
10．计算：（1）（2x-$\frac{1}{3}$）（x+3）
（2）[（x-y）（x+y）-（x+y）2]÷（-2y）
分析 （1）利用多项式的乘法法则即可求解；
（2）首先利用平方差公式和完全平方公式计算括号内的式子，然后利用多项式与单项式的除法法则求解．
解答 解：（1）原式=2x2+6x-$\frac{1}{3}$x-1=2x2+$\frac{17}{3}x$-1；
（2）原式=【x2-y2-（x2+y2+2xy）】÷（-2y）
={-2y2-2xy）÷（-2y）
=y+x．
点评 本题主要考查完全平方公式的运用，熟记公式是解题的关键．
练习册系列答案
相关题目
18．
观察两个函数y1和y2的图象，当x=1时，这两个函数的函数值的大小关系为（ ）
观察两个函数y1和y2的图象，当x=1时，这两个函数的函数值的大小关系为（ ）| A． | y1＞y2 | B． | y1＜y2 | C． | y1=y2 | D． | 不确定 |
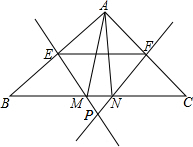如图，在△ABC中，∠BAC＞90°，AB=AC，AB的垂直平分线EM交BC于M，AC的垂直平分线FN交BC于N，EM交FN于P．
2．若一个数的相反数是5，则这个数是（ ）
| A． | 5 | B． | $\frac{1}{5}$ | C． | -$\frac{1}{5}$ | D． | -5 |
