题目内容
15.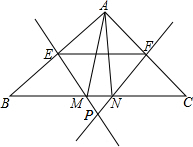 如图,在△ABC中,∠BAC>90°,AB=AC,AB的垂直平分线EM交BC于M,AC的垂直平分线FN交BC于N,EM交FN于P.
如图,在△ABC中,∠BAC>90°,AB=AC,AB的垂直平分线EM交BC于M,AC的垂直平分线FN交BC于N,EM交FN于P.(1)求证:△PMN是等腰三角形;
(2)连接AM,AN和EF,试探索△AEF与△AMN周长间的大小关系.
分析 (1)由AB=AC,可得∠B=∠C,又由AB的垂直平分线EM交BC于M,AC的垂直平分线FN交BC于N,可得∠PMN=∠BME=90°-∠B,∠PNM=∠CNF=90°-∠C,继而证得△PMN是等腰三角形;
(2)由AB的垂直平分线EM交BC于M,AC的垂直平分线FN交BC于N,可得△AMN周长=BC,△AEF的周长大于BC,即可求得△AEF与△AMN周长间的大小关系.
解答 (1)证明:∵AB=AC,
∴∠B=∠C,
∵AB的垂直平分线EM交BC于M,AC的垂直平分线FN交BC于N,
∴∠PMN=∠BME=90°-∠B,∠PNM=∠CNF=90°-∠C,
∴∠PMN=∠PNM,
∴PM=PN,
即△PMN是等腰三角形;
(2)△AEF的周长大于△AMN的周长.
理由:∵AB的垂直平分线EM交BC于M,AC的垂直平分线FN交BC于N,
∴AM=BM,AN=CN,AE=$\frac{1}{2}$AB,AF=$\frac{1}{2}$AC,
∴△AMN的周长为:AM+MN+AN=BM+MN+CN=BC,EF=$\frac{1}{2}$BC,
∵AB+AC>BC,
∴$\frac{1}{2}$AB+$\frac{1}{2}$AC>$\frac{1}{2}$BC,
∴AE+AF>$\frac{1}{2}$BC,
∴AE+AF+EF>$\frac{1}{2}$BC+$\frac{1}{2}$BC=BC,
∴△AEF的周长大于△AMN的周长.
点评 此题考查了线段垂直平分线的性质以及等腰三角形的判定与性质.注意比较△AEF与△AMN周长间的大小关系时,找到BC和它们的关系是关键.

练习册系列答案
相关题目
3.若(x-6)(x+p)=x2+2mx+36,则p、m的值分别是( )
| A. | -6,-6 | B. | -6,-12 | C. | 6,0 | D. | 6,6 |
7. 如图,从点O出发的五条射线OA,OB,OC,OD,OE,可组成锐角的个数是( )
如图,从点O出发的五条射线OA,OB,OC,OD,OE,可组成锐角的个数是( )
 如图,从点O出发的五条射线OA,OB,OC,OD,OE,可组成锐角的个数是( )
如图,从点O出发的五条射线OA,OB,OC,OD,OE,可组成锐角的个数是( )| A. | 4个 | B. | 6个 | C. | 8个 | D. | 10个 |
5.已知点(3,y1),(-1,y2),(2,y3)在反比例函数$y=\frac{4}{x}$的图象上,则( )
| A. | y1>y2>y3 | B. | y1<y2<y3 | C. | y2<y1<y3 | D. | y3<y1<y2 |
 如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象.
如图,在同一平面直角坐标系中画出函数y=$\frac{1}{2}$x2和y=2x2的图象.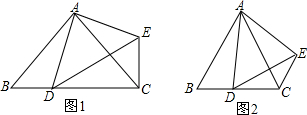
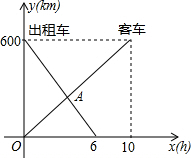 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车从两地同时出发,设客车离开甲地的距离为y1(km),出租车离开甲地的距离为y2(km),客车行驶的时间为x(h),y1、y2与x的函数关系图象如图所示:
一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车从两地同时出发,设客车离开甲地的距离为y1(km),出租车离开甲地的距离为y2(km),客车行驶的时间为x(h),y1、y2与x的函数关系图象如图所示: