题目内容
20．请你画一个三角形，并将这个三角形的面积四等分．分析 将一边四等分，把分点与这边相对的顶点连接，根据等底同高的三角形的面积相等可得符合条件．
解答 
解：如图所示，在△ABC的BC边上取四等分点D，E，F，连接AD，AE，AF，
则S△ABD=S△ADE=S△AEF=S△AFC=$\frac{1}{4}$S△ABC．
点评 本题考查了三角形的面积，三角形的一条中位线把三角形分成2个相似三角形，其中小三角形的面积为大三角形面积的$\frac{1}{4}$；等底同高的三角形的面积相等．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
求阴影部分的面积．
11．在△ABC中，AB=AC．
（1）若D为AC的中点，BD把三角形的周长分别24cm和30cm两部分，求△ABC三边的长．
（2）若D为AC上一点，试说明AC＞$\frac{1}{2}$（BD+DC）
（1）若D为AC的中点，BD把三角形的周长分别24cm和30cm两部分，求△ABC三边的长．
（2）若D为AC上一点，试说明AC＞$\frac{1}{2}$（BD+DC）
5．-（-2）的值是（ ）
| A． | -2 | B． | 2 | C． | ±2 | D． | 4 |
12．一个二次函数，当x=0时，y=-5，当x=-1时，y=-4，当x=2时，y=5，则这个二次函数的解析式是（ ）
| A． | y=2x2-x-5 | B． | y=2x2+x+5 | C． | y=2x2-x+5 | D． | y=2x2+x-5 |
10．
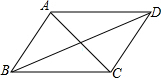如图，已知四边形ABCD是平行四边形，下列结论中不一定正确的是（ ）
如图，已知四边形ABCD是平行四边形，下列结论中不一定正确的是（ ）| A． | 当AB=AD时，它是菱形 | B． | 当AC=BD时，它是矩形 | ||
| C． | 当AC⊥BD时，它是菱形 | D． | 当∠ABC=90°时，它是正方形 |