题目内容
11.(1)解方程:x2-2x-15=0;(2)先化简,再求值:$\frac{{x}^{2}-2x+1}{{x}^{2}-x}$+$\frac{2-x}{x}$,其中x=$\sqrt{2}$-1.
分析 (1)利用因式分解法求出x的值即可;
(2)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:(1)原方程可化为(x+3)(x-5)=0,
解得x1=-3,x2=5;
(2)原式=$\frac{x-1}{x}$+$\frac{2-x}{x}$
=$\frac{x-1+2-x}{x}$
=$\frac{1}{x}$,
当x=$\sqrt{2}$-1时,原式=$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列等式中y是x的反比例函数的是( )
| A. | y=4x | B. | $\frac{y}{x}$=3 | C. | y=6x+1 | D. | xy=2 |
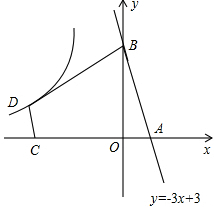 如图,直线l:y=-3x+3与x轴,y轴交于A,B两点,CD∥AB,且AB=3CD,AB⊥BD,BD⊥CD,双曲线y=$\frac{k}{x}$过D点,求k的值.
如图,直线l:y=-3x+3与x轴,y轴交于A,B两点,CD∥AB,且AB=3CD,AB⊥BD,BD⊥CD,双曲线y=$\frac{k}{x}$过D点,求k的值.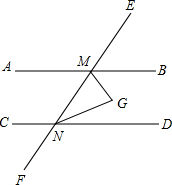 如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,完成下面的证明:
如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,完成下面的证明: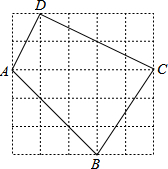 如图,每个小方格都是边长为1的正方形.
如图,每个小方格都是边长为1的正方形.