题目内容
12. 如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点A(0,-1),B(3,2)
如图,在平面直角坐标系xOy中,抛物线y=x2+mx+n经过点A(0,-1),B(3,2)(1)求抛物线的表达式及对称轴;
(2)设点B关于原点的对称点为B′,点C是抛物线对称轴上一动点,记抛物线在A、B之间的部分为图象G(包含A、B两点),若直线B′C与图象G有公共点,结合函数图象,求点C的纵坐标t的取值范围.
分析 (1)将A与B坐标代入抛物线解析式求出m与n的值,确定出抛物线解析式,求出对称轴即可;
(2)由题意确定出B′坐标,以及二次函数的最小值,确定出C纵坐标的最小值,求出直线BB′解析式,令x=1求出y的值,即可确定出t的范围.
解答 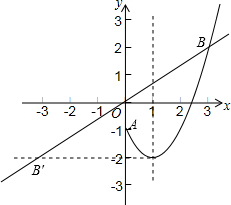 解:(1)∵抛物线y=x2+mx+n经过点A(0,-1),B(3,2),
解:(1)∵抛物线y=x2+mx+n经过点A(0,-1),B(3,2),
代入得:$\left\{\begin{array}{l}{-1=n}\\{2=9+3m+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=-2}\\{n=-1}\end{array}\right.$.
∴抛物线解析式为y=x2-2x-1,对称轴为直线x=1;
(2)∵B(3,2),
∴B′(-3,-2).
由函数图象得出C纵坐标最小值为-2.
设直线BB′的解析式为y=kx+b,
则$\left\{\begin{array}{l}{2=3k+b}\\{-2=-3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=0}\end{array}\right.$.
∴直线BB′的解析式为y=$\frac{2}{3}$x,
当x=1时,y=$\frac{2}{3}$,
结合函数图象可知t的范围为-2≤t≤$\frac{2}{3}$.
点评 此题考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,以及函数的最值,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
3.对于函数y=$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在第一、三象限 | B. | 当x>0时,y的值随x的增大而增大 | ||
| C. | 它的图象与直线y=-x无交点 | D. | 当x<0时,y的值随x的增大而减小 |
20.下列说法中,正确的是( )
| A. | 负数没有立方根 | B. | 一个数的立方根有两个 | ||
| C. | ($\root{3}{a}$)3=a | D. | $\root{3}{a}$<a |
7.直线y=x+m和抛物线y=x2+bx+c都经过点A(1,0),B(3,2),则不等式x2+bx+c>x+m的解集为( )
| A. | 0<x<2 | B. | x<2 | C. | 0<x<3 | D. | x<1或x>3 |
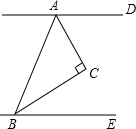 如图,直线AD∥BE,AC、BC分别平分∠BAD、∠ABE,∠CAD=55°,则∠CBE=35°.
如图,直线AD∥BE,AC、BC分别平分∠BAD、∠ABE,∠CAD=55°,则∠CBE=35°.