��Ŀ����
����Ŀ���������������������ʽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
С������ѧϰ���κ����ľ��飬������������Щ��������ʽ���ص㣬�о������ǵ�ͼ������ʡ�������С���ķ������о����̣��벹��������
��1���۲�������Щ��������ʽ�����Ƕ����й�ͬ���ص㣬���Ա�ʾΪ����![]() _______������xΪ�Ա�����
_______������xΪ�Ա�����
��2����ͼ����ƽ��ֱ������ϵ![]() �У������˺���
�У������˺���![]() �IJ���ͼ������㷨�����������ͼ��������
�IJ���ͼ������㷨�����������ͼ��������
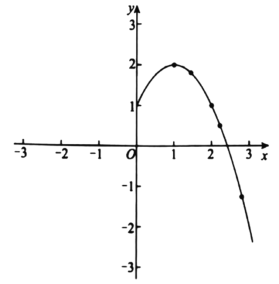
��3������������Щ�����������ĸ����ۣ�
�ٺ���ͼ�����y��Գ�
����Щ�����������ֵ��ͬʱҲ����Сֵ
�۴���ij����������![]() ��mΪ������ʱ��y��x�����������
��mΪ������ʱ��y��x�����������![]() ʱ��y��x���������С
ʱ��y��x���������С
�ܺ���ͼ����x�ṫ����ĸ���ֻ������0����2����4��
������ȷ���۵������________��
��4����Ϻ���ͼ������⣺������x�ķ���![]() ��һ��ʵ����Ϊ3����÷���������ʵ����Ϊ_______��
��һ��ʵ����Ϊ3����÷���������ʵ����Ϊ_______��
���𰸡���1��![]() ��a��0������2��ͼ�����⣻��3���٢ۣ���4��
��a��0������2��ͼ�����⣻��3���٢ۣ���4��![]()
��������
��1���۲��������κ�������ʽ���ص㣬��֪�����Ƕ����й�ͬ���ص㣺һ�����x���о���ֵ�����ɣ�
��2�����������ֵ����x<0ʱ��![]() ��������㷨������ͼ����.
��������㷨������ͼ����.
��3������������κ����Ķ�ͼ�κ����ʣ���һ�жϣ����ɣ�
��4�������k��ֵ������![]() ��
�� ![]() ����ͬһ����ϵ�У�����ͼ������������ͼ��Ľ������꣬���ɵõ���.
����ͬһ����ϵ�У�����ͼ������������ͼ��Ľ������꣬���ɵõ���.
��1���۲��������κ�������ʽ���ص㣬��֪�����Ƕ����й�ͬ���ص㣺һ�����x���о���ֵ������![]() ��a��0����
��a��0����
�ʴ��ǣ�![]() ��a��0����
��a��0����
��2����x<0ʱ��![]() ��������㷨����ͼ��ʾ��
��������㷨����ͼ��ʾ��
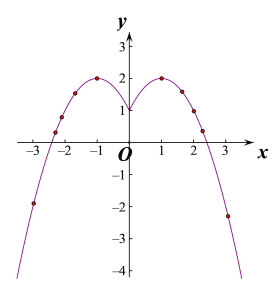
��3����![]() ��
��![]() ������y��Գƣ�
������y��Գƣ�
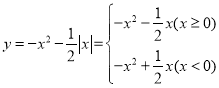 ��ͼ�����y��Գƣ�
��ͼ�����y��Գƣ�
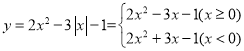 ��ͼ�����y��Գƣ�
��ͼ�����y��Գƣ�
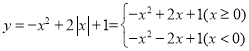 ��ͼ�����y��Գƣ�
��ͼ�����y��Գƣ�
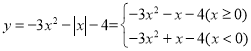 ��ͼ�����y��Գƣ�
��ͼ�����y��Գƣ�
�����ȷ��
��![]() ������Сֵ��û�����ֵ��
������Сֵ��û�����ֵ��
![]() ������Сֵ��û�����ֵ��
������Сֵ��û�����ֵ��
![]() �������ֵ��û����Сֵ��
�������ֵ��û����Сֵ��
![]() ������Сֵ��û�����ֵ��
������Сֵ��û�����ֵ��
![]() �������ֵ��û����Сֵ��
�������ֵ��û����Сֵ��
![]() �������ֵ��û����Сֵ��
�������ֵ��û����Сֵ��
��ڴ���
�� ��ͼ�����y��Գƣ�
��ͼ�����y��Գƣ�
��![]() ʱ��y��x�����������
ʱ��y��x�����������![]() ʱ��y��x���������С��
ʱ��y��x���������С��
�����ȷ��
��![]() ��ͼ����x����1�������㣬
��ͼ����x����1�������㣬
![]() ��ͼ����x��û�й����㣬
��ͼ����x��û�й����㣬
![]() ��ͼ����x����1�������㣬
��ͼ����x����1�������㣬
![]() ��ͼ����x����2�������㣬
��ͼ����x����2�������㣬
![]() ��ͼ����x����2�������㣬
��ͼ����x����2�������㣬
![]() ��ͼ����x��û�й����㣬
��ͼ����x��û�й����㣬
��ܴ���
�ʴ��ǣ��٢ۣ�
��4���߹���x�ķ���![]() ��һ��ʵ����Ϊ3��
��һ��ʵ����Ϊ3��
��![]() ����ã�k=1��
����ã�k=1��
��![]() ��
�� ![]() ��
��
����ͼ����ͼ��ʾ��
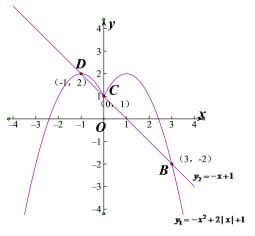
�����x�ķ���![]() ����������ʵ����Ϊ��
����������ʵ����Ϊ��![]() ��
��
�ʴ��ǣ�![]()

 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д� ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�