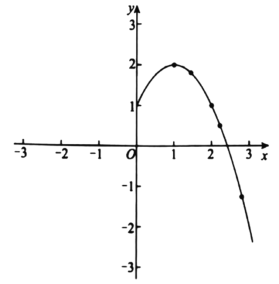题目内容
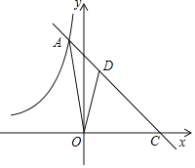
【题目】如图,在平面直角坐标系xOy中,函数y=﹣x+5的图象与函数y=![]() (k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(k<0)的图象相交于点A,并与x轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求k的值;
(2)根据图象,直接写出当x<0时不等式![]() >﹣x+5的解集;
>﹣x+5的解集;
(3)求△AOD的面积.
【答案】(1)k=﹣6;(2)﹣1<x<0;(3)5.
【解析】
(1)过A作AM⊥x轴于M,先求出点C的坐标,再根据S△AOC=15,求出点A的坐标,进而即可得到k的值;
(2)由函数的图象,可知:反比例函数图象在一次函数图象上方部分所对应的x的范围,即为不等式![]() >﹣x+5的解集;
>﹣x+5的解集;
(3)由△AOD与△AOC的高相等,CD:AC=2:3,进而求解.
(1)对于y=﹣x+5,当y=0时,x=5,
即OC=5,C点的坐标是(5,0),
过A作AM⊥x轴于M,
∵S△AOC=15,
∴![]() =15,解得:AM=6,
=15,解得:AM=6,
∴A点的纵坐标是6,
把y=6代入y=﹣x+5得:x=﹣1,
即A点的坐标是(﹣1,6),
把A点的坐标代入y=![]() 得:k=﹣6;
得:k=﹣6;
(2)由函数图象可知:当﹣1<x<0时,![]() >﹣x+5,
>﹣x+5,
∴当x<0时不等式![]() >﹣x+5的解集是:﹣1<x<0;
>﹣x+5的解集是:﹣1<x<0;
(3)∵CD:AC=2:3,S△AOC=15,
∴△AOD的面积=![]() S△AOC=
S△AOC=![]() =5.
=5.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】我市某校组织“学经典,用经典”知识竞赛,每班参加比赛的学生人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为
四个等级,其中相应等级的得分依次记为![]() 分,
分,![]() 分,
分,![]() 分,
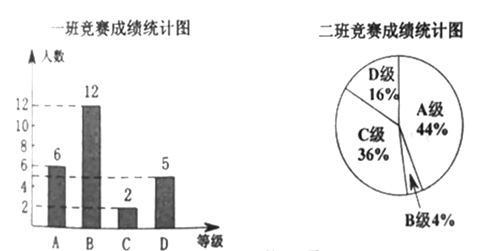
分,![]() 分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
分,学校将某年级的一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩“![]() 级”的人数为 ;
级”的人数为 ;
(2)请你将下表补充完整:
平均数(分) | 中位数(分) | 众数(分) | |
一班 |
|
| |
二班 |
|
|
(3)请你对这次两班成绩统计数据的结果进行分析(写出一条结论即可)
【题目】安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全区范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽部分使用电瓶车的市民,就骑电瓶车戴安全帽情况(![]() :每次戴、
:每次戴、![]() :经常戴、
:经常戴、![]() :偶尔戴、
:偶尔戴、![]() :都不戴)进行问卷调查,将相关的数据制成如下统计图表.
:都不戴)进行问卷调查,将相关的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 | 人数 |
| 68 |
| 245 |
| 510 |
| 177 |
合计 | 1000 |
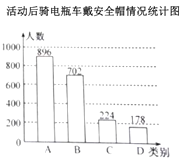
(1)宣传活动前,在抽取的市民中哪一类别的人数最多?占抽取人数的百分之几?
(2)该区约有37万人使用电瓶车,请估计活动前全市骑电瓶车“都不戴”安全帽的总人数;
(3)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理?请结合统计图表,谈谈你对交警部门宣传活动的效果的看法.