题目内容
17.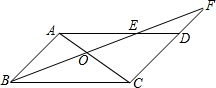 如图,在?ABCD中,E在AD上,BE和CD延长线交于点F,若BO=4,EO=3,则EF=$\frac{7}{3}$.
如图,在?ABCD中,E在AD上,BE和CD延长线交于点F,若BO=4,EO=3,则EF=$\frac{7}{3}$.
分析 首先证得△AOE∽△COB,得出$\frac{AO}{OC}$=$\frac{EO}{BO}$=$\frac{3}{4}$,进一步证得△AOB∽△COF,得出$\frac{BO}{OF}$=$\frac{AO}{OC}$,求得OF,得出BF,进一步求得EF即可.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴△AOE∽△COB,
∴$\frac{AO}{OC}$=$\frac{EO}{BO}$=$\frac{3}{4}$,
∴△AOB∽△COF,
∴$\frac{BO}{OF}$=$\frac{AO}{OC}$,
即$\frac{4}{OF}$=$\frac{3}{4}$,
∴OF=$\frac{16}{3}$,
∴EF=OF-OE=$\frac{16}{3}$-3=$\frac{7}{3}$.
故答案为:$\frac{7}{3}$.
点评 此题考查三角形的相似的判定与性质,平行四边形的性质,掌握相似三角形的判定方法是解决问题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
7.下列说法中正确的是( )
| A. | 横坐标为0的点在x轴上 | |
| B. | 点M(-3,-5)到x轴的距离为-5 | |
| C. | 在平面直角坐标系内,点A(1,-4)和点B(-4,1)表示同一个点 | |
| D. | 若a=0,则点P(2,a)在x轴上 |
8.菱形具有而矩形不一定具有的性质是( )
| A. | 两条对角线相等 | B. | 两条对角线互相垂直 | ||
| C. | 两条对角线互相平分 | D. | 两组对边分别相等 |
7.等腰三角形的底和腰是方程x2-7x+12=0的两个根,则这个三角形的周长是( )
| A. | 11 | B. | 10 | C. | 11或10 | D. | 不能确定 |
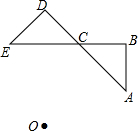 如图,△ABC绕点O逆时针旋转45°得△CDE,A旋转到点C,点C旋转到点E,点B旋转到点D,其中A、C、D三点共线,B、C、E三点共线.
如图,△ABC绕点O逆时针旋转45°得△CDE,A旋转到点C,点C旋转到点E,点B旋转到点D,其中A、C、D三点共线,B、C、E三点共线.