题目内容
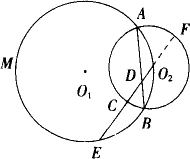
已知如下图,⊙O与⊙![]() 外切于P点,AB是外公切线,OA=3,
外切于P点,AB是外公切线,OA=3,![]() B=9,求阴影部分的面积.
B=9,求阴影部分的面积.

答案:
解析:
解析:
|
简解:连结O ∵⊙O和⊙ ∴O 又 ∴∠ ∴∠AOP=90°+30°=120°, OC=O ∴S阴暗= 分析:因OA∥ 点评:对于面积的计算,要注意观察图形中面积相等(或成比例)的三角形,当题目中有平行线时,常出现同底等高的三角形(上题中的△ACD和△BCD,△ABD和△ABC),当题目中有共顶点的三角形时,常出现面积成比例的三角形(上题中的△DCE和△ECB,等),然后利用面积关系进行计算.对不规则图形面积的计算,注意观察图形与其他图形的关系,转化为规则图形面积的计算. |

练习册系列答案
相关题目
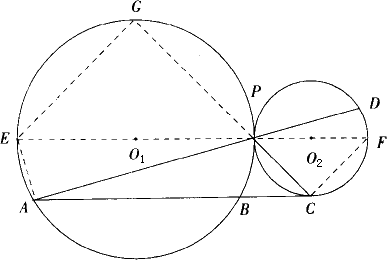

 ,求EF的长;
,求EF的长; 