Question

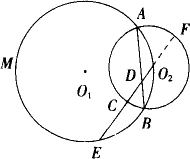
已知如下图，⊙O与⊙P相交于A、B两点，点P在⊙O上，⊙O的弦AC切⊙P于点A，CP及其延长线交⊙P于D、E，过点F作EF⊥CE，交CB的延长线于F。
（1）求证：BC是⊙P的切线；
（2）若CD=2，CB=2，求EF的长；
（3）若设k=PE∶CE，是否存在实数k，使△PBD恰好是等边三角形，若存在，求出k的值；若不存在， 请说明理由。

Answer 1

解：（1）连接PA、PB；
∵AC切⊙P于A，PA是⊙P的半径，
∴AC⊥PA，即∠PAC=90°
又∵四边形PACB接于⊙O
∴∠ PBC+∠PAC=180°
∴∠PBC=90°，
即PB⊥CB，
∴BC是⊙P的切线；
（2）连BD、BE则∠DBC+∠DBP=90°，∠BDP+∠BED=90°
又∵PB=PD
∴∠PBD=∠PDB
∴∠DBC=∠BEC
∴△CBD∽△CEB
∴BC²=CD·CE
∴CE=4，DE=4-2=2
∴PB=1，
∵∠ECF=∠BCP
∴△EFC∽△BPC
∴
∴EF=
（3）存在实数k，使△PBD为等边三角形，


CE=3PEPE∶CE=1∶3
即：k=时，△PBD为等边三角形。