题目内容
14.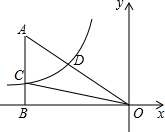 如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB与相交于点C.若△COD的面积为6,则k的值为-8.
如图,已知双曲线y=$\frac{k}{x}$(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB与相交于点C.若△COD的面积为6,则k的值为-8.
分析 设D(t,$\frac{k}{t}$),利用点D为OA的中点得到A(2t,$\frac{2k}{t}$),接着表示出C(2t,$\frac{k}{2t}$),然后根据三角形面积公式得到$\frac{1}{2}$•($\frac{2k}{t}$-$\frac{k}{2t}$)•(-2t)-$\frac{1}{2}$•($\frac{2k}{t}$-$\frac{k}{2t}$)•(t-2t)=6,再解关于k的方程即可.
解答 解:设D(t,$\frac{k}{t}$),
∵点D为OA的中点,
∴A(2t,$\frac{2k}{t}$),
∵AB⊥x轴,
∴C点的横坐标为2t,
∴C(2t,$\frac{k}{2t}$),
∴S△COD=S△OAC-S△ACD=$\frac{1}{2}$•($\frac{2k}{t}$-$\frac{k}{2t}$)•(-2t)-$\frac{1}{2}$•($\frac{2k}{t}$-$\frac{k}{2t}$)•(t-2t)=6,
∴k=-8.
故答案为:-8.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.

练习册系列答案
相关题目
4.若a>b,则下列式子正确的是( )
| A. | a-4>b-3 | B. | $\frac{1}{2}$a<$\frac{1}{2}$b | C. | -3a>-3b | D. | 3+2a>3+2b |
 (1)在直角坐标系描出(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)并将各点用线段依次连接起来.
(1)在直角坐标系描出(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)并将各点用线段依次连接起来.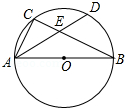 如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为$\frac{14}{5}$.
如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为$\frac{14}{5}$.