题目内容
13．无论m为什么实数，直线y=mx+m-2总经过点（-1，-2）．分析 利用m（x+1）-y-2=0，经过x+1=0和-y-2=0的交点来求出该点的坐标．
解答 解：直线mx-y+m-2=0 即 m（x+1）-y-2=0，经过x+1=0和-y-2=0的交点（-1，-2）
∴无论m为什么实数，直线y=mx+m-2总经过点（-1，-2）．
故答案为：（-1，-2）．
点评 本题考查了直线过定点问题，判断m（x+1）-y-2=0，经过x+1=0和-y-2=0的交点，是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在菱形ABCD中，AC与BD相交于点O，点P是AB的中点，PO=5，则菱形ABCD的周长是40．
4．
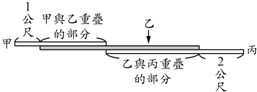如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形．已知乙有一部分只与甲重迭，其余部分只与丙重迭，甲没有与乙重迭的部分的长度为1公尺，丙没有与乙重迭的部分的长度为2公尺．若乙的长度最长且甲、乙的长度相差x公尺，乙、丙的长度相差y公尺，则乙的长度为多少公尺？（ ）
如图为甲、乙、丙三根笔直的木棍平行摆放在地面上的情形．已知乙有一部分只与甲重迭，其余部分只与丙重迭，甲没有与乙重迭的部分的长度为1公尺，丙没有与乙重迭的部分的长度为2公尺．若乙的长度最长且甲、乙的长度相差x公尺，乙、丙的长度相差y公尺，则乙的长度为多少公尺？（ ）| A． | x+y+3 | B． | x+y+1 | C． | x+y-1 | D． | x+y-3 |
18．在一次捐款活动中，某单位共有13人参加捐款，其中小王捐款数比13人捐款的平均数多2元，据此可知，错误的是（ ）
| A． | 小王的捐款数不可能最少 | |
| B． | 小王的捐款数可能最多 | |
| C． | 将捐款数按从少到多排列，小王的捐款数可能排在第十二位 | |
| D． | 将捐款数按从少到多排列，小王的捐款数一定比第七名多 |
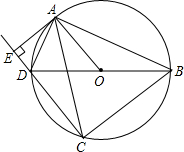如图所示，四边形ABCD是⊙O的内接四边形，AB=AC，BD是⊙O的直径，延长CD，过点A作AE⊥CD于点E．
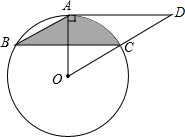如图，⊙O经过?ABCD的三个顶点A，B，C，且圆心O在DC的延长线上，∠D=30°，AD=6$\sqrt{3}$cm．