题目内容
 如图,直线AB,CD,EF相交于点O,∠AOF=120°,∠BOD=90°,求∠BOF,∠EOC的度数.
如图,直线AB,CD,EF相交于点O,∠AOF=120°,∠BOD=90°,求∠BOF,∠EOC的度数.考点:对顶角、邻补角
专题:
分析:首先根据邻补角的性质可得∠AOD的度数,再根据∠AOF=120°可得∠DOF的度数,再利用余角的定义可得∠BOF的度数,最后根据对顶角相等可得∠EOC的度数.
解答:解:∵∠BOD=90°,
∴∠AOD=180°-90°=90°,
∵∠AOF=120°,
∴∠DOF=120°-90°=30°,
∴∠BOF=90°-30°=60°,
∠EOC=∠DOF=30°.
∴∠AOD=180°-90°=90°,
∵∠AOF=120°,
∴∠DOF=120°-90°=30°,
∴∠BOF=90°-30°=60°,
∠EOC=∠DOF=30°.
点评:此题主要考查了邻补角和对顶角,关键是掌握邻补角互补,对顶角相等.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究在第n个图中,黑、白瓷砖分别各有多少块( )


| A、4n+6,n(n+1) |
| B、4n+6,n(n+2) |
| C、n(n+1),4n+6 |
| D、n(n+2),4n+6 |
抛物线y=-3(x+2)2-4的开口方向和顶点坐标分别是( )
| A、向上,(2,-4) |
| B、向上,(-2,-4) |
| C、向下,(2,-4) |
| D、向下,(-2,-4) |
在函数y=(x+1)2+3中,y随x增大而减小,则x的取值范围为( )
| A、x>-1 | B、x>3 |
| C、x<-1 | D、x<3 |
在式子m+5、ab、a+b<1、x、-ah、s=ab中代数式的个数有( )
| A、6个 | B、5个 | C、4个 | D、3个 |
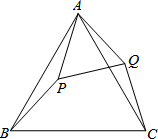 如图,等边△ABC,点P在△ABC内,点Q在△ABC外,分别联结AP、BP、AQ、CQ,∠ABP=∠ACQ,BP=CQ.
如图,等边△ABC,点P在△ABC内,点Q在△ABC外,分别联结AP、BP、AQ、CQ,∠ABP=∠ACQ,BP=CQ. 如图,直线y=2x-2分别交x轴、y轴于B、A两点,交双曲线y=
如图,直线y=2x-2分别交x轴、y轴于B、A两点,交双曲线y=