题目内容
 如图,已知等腰△ABC的面积为16cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面为
如图,已知等腰△ABC的面积为16cm2,点D,E分别是AB,AC边的中点,则梯形DBCE的面为考点:相似三角形的判定与性质,三角形中位线定理
专题:
分析:根据三角形的中位线得出DE=
BC,DE∥BC,推出△ADE∽△ABC,求出它们的面积比,即可求出答案.
| 1 |
| 2 |
解答:解:∵点D、E分别是AB、AC边的中点,
∴DE=BC,DE∥BC,
∴△ADE∽△ABC,
∴
=
∵等腰△ABC的面积为16cm2,
∴△ADE的面积是4cm2,
∴梯形DBCE的面积为16-4=12(cm2),
故答案为:12.
∴DE=BC,DE∥BC,
∴△ADE∽△ABC,
∴
| S△ADE |
| S△ABC |
| 1 |
| 4 |
∵等腰△ABC的面积为16cm2,
∴△ADE的面积是4cm2,
∴梯形DBCE的面积为16-4=12(cm2),
故答案为:12.
点评:本题考查了三角形的中位线和相似三角形的性质和判定的应用,解此题的关键是求出两个三角形面积的比值,题型较好,但是一道比较容易出错的题目.

练习册系列答案
相关题目
 如图,在△ABC中,点D、E分别为边AB、AC上的点,且DE∥BC,若AD=5,BD=10,AE=3,则CE的长为( )
如图,在△ABC中,点D、E分别为边AB、AC上的点,且DE∥BC,若AD=5,BD=10,AE=3,则CE的长为( )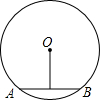 如图,AB是⊙O的一条弦,AB=6,圆心O到AB的距离为4,则⊙O的半径为
如图,AB是⊙O的一条弦,AB=6,圆心O到AB的距离为4,则⊙O的半径为 在学习了几何中的对称知识以后,拉拉忽然想起了以前做过的一道题:有一组数排成方阵,如图,试计算这组数的和.拉拉想,方阵就像正方形,正方形是轴对称图形,也是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题呢?拉拉试了试,竟得到了非常巧妙的方法.你也来试试看.
在学习了几何中的对称知识以后,拉拉忽然想起了以前做过的一道题:有一组数排成方阵,如图,试计算这组数的和.拉拉想,方阵就像正方形,正方形是轴对称图形,也是中心对称图形,能不能利用轴对称和中心对称的思想来解决方阵的计算问题呢?拉拉试了试,竟得到了非常巧妙的方法.你也来试试看.