题目内容
18.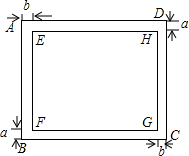 如图,矩形ABCD的长为100cm、宽为80cm,在它的内部有一个矩形EFGH(EH>EF).设AD与EH之间的距离、BC与FG之间的距离都为a cm,AB与EF之间的距离、DC与HG之间的距离郡为b cm.
如图,矩形ABCD的长为100cm、宽为80cm,在它的内部有一个矩形EFGH(EH>EF).设AD与EH之间的距离、BC与FG之间的距离都为a cm,AB与EF之间的距离、DC与HG之间的距离郡为b cm.(1)当a、b满足什么关系时,两个矩形相似?
(2)若b比a大1,且两个矩形相似,求矩形EFGH的面积.
分析 (1)根据相似多边形的性质即可得到结论;
(2)根据相似多边形的性质求出a=4,b=5,然后根据矩形的面积公式求得结果.
解答 解:(1)当两个矩形相似,
则$\frac{100}{100-2b}=\frac{80}{80-2a}$,
∴$\frac{a}{b}$=$\frac{4}{5}$,
∴当$\frac{a}{b}$=$\frac{4}{5}$时,两个矩形相似;
(2)∵b比a大1,且两个矩形相似,
由(1)得:当$\frac{a}{b}$=$\frac{4}{5}$时,两个矩形相似,
∴$\frac{a}{b}=\frac{a}{a+1}=\frac{4}{5}$,
∴a=4,b=5,
∴矩形EFGH的面积=(100-2×5)(80-2×4)=6480.
点评 本题考查了相似多边形的性质,矩形的面积的求法,熟练掌握相似多边形的性质是解题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
6.下列说法正确的是( )
| A. | 两个数相加的和一定大于其中一个加数 | |
| B. | 两个有理数相加同号得正,异号得负 | |
| C. | 两个负数相加,和取负,并把绝对值相减 | |
| D. | 两个数相加的和可能为零 |
16.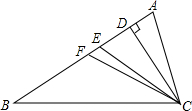 如图,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
如图,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
 如图,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )
如图,CD、CE、CF分别是△ABC的高、角平分线、中线,则下列各式中错误的是( )| A. | BA=2BF | B. | ∠ACE=$\frac{1}{2}$∠ACB | C. | AE=BE | D. | CD⊥AB |
 用锤子以均匀的力敲铁钉进入木板,随着铁钉的进入,铁钉所受的阻力也会越来起大,设每次进入木板的钉子长度为前-次进人木板的长度的x,其中0<x<1(第一次除外),已知某人敲击第一次受敲击后进入木板部分的铁钉长度为钉长的$\frac{4}{7}$,某人敲击三次完全钉入木板中,求x的值.
用锤子以均匀的力敲铁钉进入木板,随着铁钉的进入,铁钉所受的阻力也会越来起大,设每次进入木板的钉子长度为前-次进人木板的长度的x,其中0<x<1(第一次除外),已知某人敲击第一次受敲击后进入木板部分的铁钉长度为钉长的$\frac{4}{7}$,某人敲击三次完全钉入木板中,求x的值.