题目内容
13．等腰梯形的上底为2cm，下底为4cm，面积为3$\sqrt{3}$cm2，则下底角的余弦值为$\frac{\sqrt{3}}{2}$．分析 过A作AE⊥BC于E，根据S梯形ABCD=$\frac{1}{2}$（AD+BC）•AE=3$\sqrt{3}$，求得AE=$\sqrt{3}$，由于梯形ABCD是等腰梯形，于是得到BE=$\frac{1}{2}$（BC-AD）=1，根据正切值求得∠B=60°，于是得到结果．
解答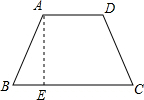 
解：如图，过A作AE⊥BC于E，
由已知得：AD=2cm．BC=4cm，
∵S梯形ABCD=$\frac{1}{2}$（AD+BC）•AE=3$\sqrt{3}$，
∴AE=$\sqrt{3}$，
∵梯形ABCD是等腰梯形，
∴BE=$\frac{1}{2}$（BC-AD）=1，
∴tan∠B=$\frac{AE}{BE}$=$\sqrt{3}$，
∴∠B=60°，
∴cos∠B=$\frac{\sqrt{3}}{2}$．
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题考查了等腰梯形的性质，解直角三角形，正确的作出辅助线构造直角三角形是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
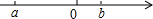a，b在数轴上如图，则：
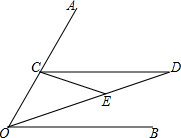已知∠AOB，点C是OA上任意一点，CD∥OB，且∠AOE=∠CEO，∠DCE=∠D，试说明∠DOB=$\frac{1}{3}$∠AOB．
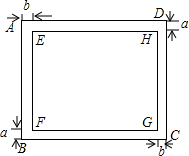如图，矩形ABCD的长为100cm、宽为80cm，在它的内部有一个矩形EFGH（EH＞EF）．设AD与EH之间的距离、BC与FG之间的距离都为a cm，AB与EF之间的距离、DC与HG之间的距离郡为b cm．