题目内容
13．如果$\left\{\begin{array}{l}{x+2y-8z=0}\\{2x-3y+5z=0}\end{array}\right.$，其中xyz≠0，那么x：y：z的值．分析 先把方程组看作关于x、y的二元一次方程组，利用加减消元法可解得x=z，y=3z，然后计算x、y、z的比值．
解答 解：$\left\{\begin{array}{l}{x+2y-8z=0①}\\{2x-3y+5z=0②}\end{array}\right.$，
①×2-②得7y-21z=0，
解y=3z，
把y=3z代入①得x+6z-8z=0，
解得x=2z，
所以x：y：z=2z：3z：z=2：3：1．
点评 本题考查了解三元一次方程组：利用代入法或加减法，把解三元一次方程组的问题转化为解二元一次方程组的问题．
练习册系列答案
相关题目
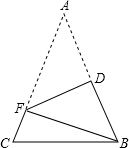如图，在△ABC中，AB=AC，AB+BC=8．将△ABC折叠，使得点A落在点B处，折痕DF分别与AB、AC交于点D、F，连接BF，则△BCF的周长是8．
4．下列计算正确的是（ ）
| A． | （-x）6+（-3x2）3=-26 | B． | （-x3）2+（-x2）3=0 | ||
| C． | （ab）2•（ab）3=a10b10 | D． | 5a2b3-3a2b2=2a2b3 |