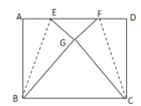
题目内容
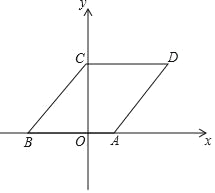
【题目】已知：在菱形ABCD中，E，F是BD上的两点，且AE∥CF．
求证：四边形AECF是菱形．
【答案】见解析
【解析】
由菱形的性质可得AB∥CD，AB＝CD，∠ADF＝∠CDF，由“SAS”可证△ADF≌△CDF，可得AF＝CF，由△ABE≌△CDF，可得AE＝CF，由平行四边形的判定和菱形的判定可得四边形AECF是菱形．
证明：∵四边形ABCD是菱形
∴AB∥CD，AB＝CD，∠ADF＝∠CDF，
∵AB＝CD，∠ADF＝∠CDF，DF＝DF
∴△ADF≌△CDF（SAS）
∴AF＝CF，
∵AB∥CD，AE∥CF
∴∠ABE＝∠CDF，∠AEF＝∠CFE
∴∠AEB＝∠CFD，∠ABE＝∠CDF，AB＝CD
∴△ABE≌△CDF（AAS）
∴AE＝CF，且AE∥CF
∴四边形AECF是平行四边形
又∵AF＝CF，
∴四边形AECF是菱形
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
