题目内容
16．
如图，已知平行四边形ABCD，延长BC至E，使CE=BC，连接AC，DE，求证：AC=DE．
分析 根据平行四边形的判定和性质定理即可得到结论．
解答 证明：∵四边形ABCD 是平行四边形，
∴AD=BC，AD∥BC，
∵CE=BC，
∴AD∥CE，AD=CE，
∴四边形ACED是平行四边形，
∴AC=DE．
点评 本题考查了平行四边形的判定和性质，熟练掌握平行四边形的判定和性质定理是解题的关键．
练习册系列答案
相关题目
6．下列运算正确的是（ ）
| A． | a3-a3=a0 | B． | a2÷a-1=a3 | C． | a2+a2=2a4 | D． | a3×a3=a3 |
如图，四边形ABCD中，AD=BC，E，F，G分别是AB、CD、AC的中点，若∠DAC=20°，∠ACB=60°，则∠FEG=20°．
4．
如图，正方形的边长为4cm，则图中阴影部分的面积为（ ）cm2．
如图，正方形的边长为4cm，则图中阴影部分的面积为（ ）cm2．| A． | 8 | B． | 16 | C． | 4 | D． | 无法确定 |
1．在-2、3.14、$\sqrt{2}$这3个数中，无理数共有（ ）
| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
8．下列是二元一次方程3x+y=4的解的是（ ）
| A． | $\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=2}\\{y=-2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ |
5．
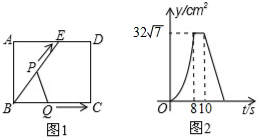如图1，E为矩形ABCD边AD上的一点，点P从点B沿折线BE-ED-DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是2cm/s．若P、Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2），已知y与t的函数关系图象如图2，则下列结论错误的是（ ）
如图1，E为矩形ABCD边AD上的一点，点P从点B沿折线BE-ED-DC运动到点C时停止，点Q从点B沿BC运动到点C时停止，它们运动的速度都是2cm/s．若P、Q同时开始运动，设运动时间为t（s），△BPQ的面积为y（cm2），已知y与t的函数关系图象如图2，则下列结论错误的是（ ）| A． | AE=12cm | B． | sin∠EBC=$\frac{\sqrt{7}}{4}$ | ||
| C． | 当0＜t≤8时，y=$\frac{\sqrt{7}}{2}$t2 | D． | 当t=9s时，△PBQ是等腰三角形 |
