题目内容
四边形ABCD为直角梯形，AD：BC=2：3，E为DC边上的中点，连接AE交BD于H点，过点H作HN⊥AD于N，NH的延长线交BC于点M，则：①AH：HE=4：3；②M为BC的中点；③S四边形BHEC-S△ABH=2S△AHD，则正确的结论有（ ）A．只有①②
B．只有①③
C．只有②③
D．①②③
【答案】分析：连结BE，过E点作EF∥BC交AB于点F，交MN于点G．
①通过求解得到S△BDE=
×S△BCD=
×
S△ABD=
S△ABD，即可作出判断；
②根据梯形中位线定理得到AD：FE：BC=2：2.5：3，从而得到BM=FG=
FE=
BC，即可作出判断；
③分别求出S△ABH，2S△AHD，S四边形BHEC与S四边形ABCD的关系，即可作出判断．
解答：
解：连结BE，过E点作EF∥BC交AB于点F，交MN于点G．
①∵E为DC边上的中点，
∴S△BDE=S△CDE，
∵AD：BC=2：3，
∴S△BDE=
×S△BCD=
×
S△ABD=
S△ABD，
即S△ABD：S△BDE=4：3，
∴AH：HE=4：3；故①正确；
②∵AH：HE=4：3，
∴FG：GE=4：3，
∵AD：BC=2：3，
∴AD：FE：BC=2：2.5：3，
∴BM=FG=
FE=
BC，
故M不为BC的中点；故②错误；
③S△ABH=
S四边形ABCD×
=
S四边形ABCD，
2S△AHD=2×
S四边形ABCD×
×
=
S四边形ABCD，
S四边形BHEC=S四边形ABCD-（
S四边形ABCD，+
S四边形ABCD×
）=
S四边形ABCD，
∵
S四边形ABCD-
S四边形ABCD=
S四边形ABCD，
∴S四边形BHEC-S△ABH=2S△AHD；故③正确．
故选B．
点评：考查了相似形综合题，涉及的知识点有平行线的性质，相似三角形的性质，梯形的性质的中位线定理，等高的三角形面积之间的关系，有一定的难度．
①通过求解得到S△BDE=
×S△BCD=×S△ABD=S△ABD，即可作出判断；②根据梯形中位线定理得到AD：FE：BC=2：2.5：3，从而得到BM=FG=
FE=BC，即可作出判断；③分别求出S△ABH，2S△AHD，S四边形BHEC与S四边形ABCD的关系，即可作出判断．
解答：
解：连结BE，过E点作EF∥BC交AB于点F，交MN于点G．①∵E为DC边上的中点，
∴S△BDE=S△CDE，
∵AD：BC=2：3，
∴S△BDE=
×S△BCD=×S△ABD=S△ABD，即S△ABD：S△BDE=4：3，
∴AH：HE=4：3；故①正确；
②∵AH：HE=4：3，
∴FG：GE=4：3，
∵AD：BC=2：3，
∴AD：FE：BC=2：2.5：3，
∴BM=FG=
FE=BC，故M不为BC的中点；故②错误；
③S△ABH=
S四边形ABCD×=S四边形ABCD，2S△AHD=2×
S四边形ABCD××=S四边形ABCD，S四边形BHEC=S四边形ABCD-（
S四边形ABCD，+S四边形ABCD×）=S四边形ABCD，∵
S四边形ABCD-S四边形ABCD=S四边形ABCD，∴S四边形BHEC-S△ABH=2S△AHD；故③正确．
故选B．
点评：考查了相似形综合题，涉及的知识点有平行线的性质，相似三角形的性质，梯形的性质的中位线定理，等高的三角形面积之间的关系，有一定的难度．
练习册系列答案
相关题目
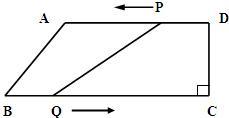23、如图，四边形ABCD为直角梯形，∠C=90°，CD=10cm，AD=30 cm，BC=36 cm，点P从D出发，以2 cm/s的速度向A运动，点Q从B同时出发，以4 cm/s的速度向C运动．其中一个点到达端点时，另一个动点也随之停止运动．
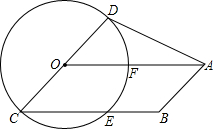如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，当CD转动时，OA固定不动，0°≤∠DOA≤90°，且总有BC∥OA，AB∥CD，若OA=4，BC与⊙O交于E，连AD，设CE为x，四边形ABCD的面积为y．
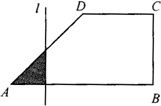四边形ABCD为直角梯形，CD∥AB，CB⊥AB且CD=BC=
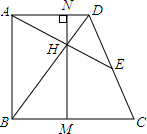四边形ABCD为直角梯形，AD：BC=2：3，E为DC边上的中点，连接AE交BD于H点，过点H作HN⊥AD于N，NH的延长线交BC于点M，则：①AH：HE=4：3；②M为BC的中点；③S四边形BHEC-S△ABH=2S△AHD，则正确的结论有（ ）
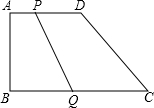四边形ABCD为直角梯形，AD∥BC，AD=36cm，BC=39cm，点P、Q分别在AD、BC上，且CQ=3AP．当AP为何值时