题目内容
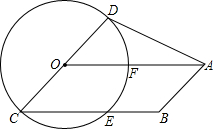 如图,⊙O半径为2,直径CD以O为中心,在⊙O所在平面内转动,当CD转动时,OA固定不动,0°≤∠DOA≤90°,且总有BC∥OA,AB∥CD,若OA=4,BC与⊙O交于E,连AD,设CE为x,四边形ABCD的面积为y.
如图,⊙O半径为2,直径CD以O为中心,在⊙O所在平面内转动,当CD转动时,OA固定不动,0°≤∠DOA≤90°,且总有BC∥OA,AB∥CD,若OA=4,BC与⊙O交于E,连AD,设CE为x,四边形ABCD的面积为y.(1)求y关于x的函数解析式,并指出x的取值范围;
(2)当x=2
| 3 |
(3)当x取何值时,四边形ABCD为直角梯形?连EF,此时OCEF变成什么图形?(只需说明结论,不必证明)
分析:(1)由于四边形ABCD不是规则的四边形,可将其分成平行四边形ABCO和△AOD两部分来求解,连接DE,过O作OH⊥BC于H,那么不难得出OH是△CDE的中位线,在直角三角形CDE中,可用直径和CE的长求出DE的值,然后即可得出OH的长,进而可根据四边形ABCD的面积计算方法求出y,x的函数关系式.下面说x的取值范围,0°≤∠DOA≤90°;因此0≤cos∠DOA≤1,而cos∠DOA=
=
;因0≤
≤1,即0≤x≤4;
(2)连接OE,那么四边形的圆内部分可分为扇形ODE和△OCE两部分,△OCE的面积容易求得;重点说明扇形ODE的面积计算方法,关键是求出圆心角∠DOE的度数;在直角三角形CDE中,CD=4,CE=2
,因此∠DCE=30°;根据圆周角定理,∠DOE=2∠DCE=60°;根据扇形的面积公式即可求出扇形ODE的面积;然后再分别计算出△OCE的面积和四边形ABCD的面积,进行比较即可.
(3)当∠CDA=90°,∠DAO=30°所以∠DCB=∠DOA=60°此时△OCE为等边三角形,所以x=2时,四边形ABCD为直角梯形,
此时OCEF变成了菱形.
| CE |
| CD |
| x |
| 4 |
| x |
| 4 |
(2)连接OE,那么四边形的圆内部分可分为扇形ODE和△OCE两部分,△OCE的面积容易求得;重点说明扇形ODE的面积计算方法,关键是求出圆心角∠DOE的度数;在直角三角形CDE中,CD=4,CE=2
| 3 |
(3)当∠CDA=90°,∠DAO=30°所以∠DCB=∠DOA=60°此时△OCE为等边三角形,所以x=2时,四边形ABCD为直角梯形,
此时OCEF变成了菱形.
解答: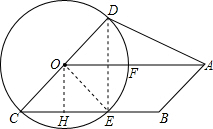 解:(1)连接DE,过O作OH⊥BC于H,则DE⊥BC,OH∥DE,
解:(1)连接DE,过O作OH⊥BC于H,则DE⊥BC,OH∥DE,
∵CD=4,CE=x,
∴DE=
=
=
,
∴OH=
DE=
,
∴y=S?ABCO+S△OAD=4×
+
×4×
,
=3
(0≤x≤4),
∴x的取值范围为0≤x≤4;
(2)当x=2
时,
∵CE=2
,CD=4,
∴DE=2,∠C=30°,
∴∠DOE=60°,OH=1,
∵S圆内部分=
+
×2
×1=
+
,
∵S四边形ABCD=3
=3
=6,
∴S圆内部分:S四边形ABCD=
,
∴四边形ABCD在圆内的面积与四边形ABCD的面积之比为(2π+3
):18;
(3)当∠CDA=90°,
由OA=2OD,得∠DAO=30°
所以∠DCB=∠DOA=60°
此时△OCE为等边三角形,所以x=2时,四边形ABCD为直角梯形,
连EF,此时OCEF变成了菱形
 解:(1)连接DE,过O作OH⊥BC于H,则DE⊥BC,OH∥DE,
解:(1)连接DE,过O作OH⊥BC于H,则DE⊥BC,OH∥DE,∵CD=4,CE=x,
∴DE=
| CD2-CE2 |
| 42-x2 |
| 16-x2 |
∴OH=
| 1 |
| 2 |
| ||
| 2 |
∴y=S?ABCO+S△OAD=4×
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=3
| 16-x2 |
∴x的取值范围为0≤x≤4;
(2)当x=2
| 3 |
∵CE=2
| 3 |
∴DE=2,∠C=30°,
∴∠DOE=60°,OH=1,
∵S圆内部分=
| 60×π×22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 2π |
| 3 |
| 3 |
∵S四边形ABCD=3
| 16-x2 |
| 16-12 |
∴S圆内部分:S四边形ABCD=
2π+3
| ||
| 18 |
∴四边形ABCD在圆内的面积与四边形ABCD的面积之比为(2π+3
| 3 |
(3)当∠CDA=90°,
由OA=2OD,得∠DAO=30°
所以∠DCB=∠DOA=60°
此时△OCE为等边三角形,所以x=2时,四边形ABCD为直角梯形,
连EF,此时OCEF变成了菱形
点评:本题主要考查了圆周角定理、平行四边形的性质、图形面积的求法、三角函数、直角梯形的判定等知识点的综合运用能力.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,半径为1的⊙D内切于圆心角为60°的扇形OAB,
如图,半径为1的⊙D内切于圆心角为60°的扇形OAB, 别是方程x2+kx+60=0的两根.
别是方程x2+kx+60=0的两根. 如图,半径为2cm,圆心角为90°的扇形OAB的
如图,半径为2cm,圆心角为90°的扇形OAB的
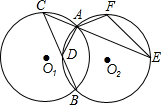 如图,半径为1的等圆⊙O1与⊙O2相交于A、B两点,点C从点A出发,在⊙O1,上逆时针运动;同时点F从点A出发,在⊙O2上顺时针运动,两点的运动速度相同,⊙O1的弦CB交⊙O2于点D.
如图,半径为1的等圆⊙O1与⊙O2相交于A、B两点,点C从点A出发,在⊙O1,上逆时针运动;同时点F从点A出发,在⊙O2上顺时针运动,两点的运动速度相同,⊙O1的弦CB交⊙O2于点D.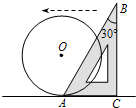 (2008•海口一模)如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为
(2008•海口一模)如图,半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A,将直角三角板沿CA边所在的直线向左平移,当平移到AB与⊙O相切时,该直角三角板平移的距离为