题目内容
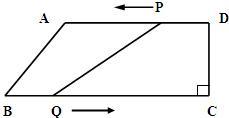 23、如图,四边形ABCD为直角梯形,∠C=90°,CD=10cm,AD=30 cm,BC=36 cm,点P从D出发,以2 cm/s的速度向A运动,点Q从B同时出发,以4 cm/s的速度向C运动.其中一个点到达端点时,另一个动点也随之停止运动.
23、如图,四边形ABCD为直角梯形,∠C=90°,CD=10cm,AD=30 cm,BC=36 cm,点P从D出发,以2 cm/s的速度向A运动,点Q从B同时出发,以4 cm/s的速度向C运动.其中一个点到达端点时,另一个动点也随之停止运动.(1)从运动开始,经过多少时间,四边形PQBA为平行四边形;
(2)从运动开始,经过多少时间,四边形PQBA为等腰梯形.
分析:(1)若四边形PQBA为平行四边形,则必须有PA=BQ,而PA、BQ均可用含t的式子来表示,所以解方程即可.
(2)若四边形PQBA为等腰梯形,则必须有BQ=PA+2(BC-AD),道理同(1),可通过解方程解决.
(2)若四边形PQBA为等腰梯形,则必须有BQ=PA+2(BC-AD),道理同(1),可通过解方程解决.
解答:(1)解:当PA=BQ时四边形PQBA为平行四边形
即30-2t=4t6t=30t=5
∴从开始运动经5s的时间,四边形PQBA为平行四边形.(6分)
(2)解:当BQ=PA+2(BC-AD)时四边形PQBA为等腰梯形
即4t=30-2t+2(36-30)6t=42t=7
∴从开始运动经5s的时间,四边形PQBA为等腰梯形.(6分)
即30-2t=4t6t=30t=5
∴从开始运动经5s的时间,四边形PQBA为平行四边形.(6分)
(2)解:当BQ=PA+2(BC-AD)时四边形PQBA为等腰梯形
即4t=30-2t+2(36-30)6t=42t=7
∴从开始运动经5s的时间,四边形PQBA为等腰梯形.(6分)
点评:此题主要考查了了平行四边形以及等腰梯形的判定,难易程度适中.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.