题目内容
5．
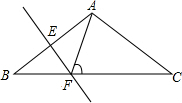如图，在△ABC中，AB=AC，∠BAC=120°，AB的垂直平分线交AB于点E，交BC于点F．连接AF，∠AFC的度数60°．
分析 先由等腰三角形的性质求出∠B的度数，再由垂直平分线的性质可得出∠BAF=∠B，由三角形内角与外角的关系即可解答．
解答 解：∵AB=AC，∠BAC=120°，
∴∠B=（180°-120°）÷2=30°，
∵EF垂直平分AB，
∴BF=AF，
∴∠BAF=∠B=30°，
∴∠AFC=∠BAF+∠B=60°．
故答案是：60°．
点评 本题考查的是线段垂直平分线的性质，即线段的垂直平分线上的点到线段的两个端点的距离相等．
练习册系列答案
名校课堂系列答案
相关题目
如图，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AC=3cm，那么AE、AC、DE这三条线段之间有怎样的数量关系？请说明理由．