题目内容
如图，把一个矩形纸片ABCD沿EF折叠后，点D、C分别落在D′、C′的位置．若∠EFB=α，则∠AED′等于
- A.α
- B.90°-α
- C.180°-α
- D.180°-2α
D
分析：根据平行线的性质及∠EFB=α可求出∠DEF的度数，再根据折叠的性质及平角的性质即可求解．
解答：∵AD∥BC，
∴∠EFB=∠DEF=α，
∵四边形ED′C′F是四边形DEFC折叠而成，
∴∠D′EF=∠DEF=α，
∴∠D′ED=2α，
∴∠AED′=180°-∠D′ED=180°-2α．
故选D．
点评：本题涉及到图形折叠的性质及平行线的性质，解答此题的关键是熟知图形折叠后与原图形全等．
分析：根据平行线的性质及∠EFB=α可求出∠DEF的度数，再根据折叠的性质及平角的性质即可求解．
解答：∵AD∥BC，
∴∠EFB=∠DEF=α，
∵四边形ED′C′F是四边形DEFC折叠而成，
∴∠D′EF=∠DEF=α，
∴∠D′ED=2α，
∴∠AED′=180°-∠D′ED=180°-2α．
故选D．
点评：本题涉及到图形折叠的性质及平行线的性质，解答此题的关键是熟知图形折叠后与原图形全等．
练习册系列答案
名校课堂系列答案
相关题目
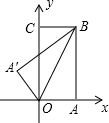如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在A′的位置上．若OB=
如图，把一个矩形纸片ABCD沿AD和BC的中点连线EF对折，要使矩形AEFB与原矩形相似，则原矩形长与宽的比为
5、如图，把一个矩形纸片ABCD沿EF折叠后，点D、C分别落在D′、C′的位置．若∠EFB=α，则∠AED′等于（ ）
如图，把一个矩形纸片ABCD沿EF折叠后，点D、C分别落在D′、C′的位置，若∠EFB=55°，则∠AED′等于（ ）
18、如图，把一个矩形纸片OABC放入平面直角坐标系中，使0A、OC分别落在x轴、y轴上，连接OB，将纸片0ABC沿OB折叠，使点A落在A′的位置上．若0A=10，AB=5，则点A′的坐标为